
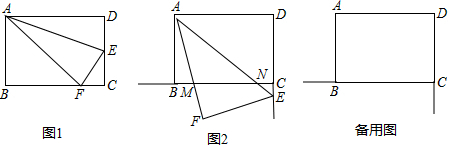
分析 (1)如图1中,①由△AEF是由△AED翻折得到,推出DE=EF,由DE+EC=DC,推出EF+EC=DC,由此即可解决问题;
②结论:△AFB∽△FEC.只要证明∠AFB=∠EFC,即可;
(2)①如图2中,结论:FM=BM+CN.只要证明△AMN是等腰三角形即可;
②如图3中,结论:FM=CN-BM.证明方法类似;
解答 解:(1)如图1中,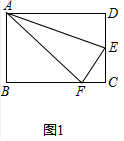
①∵△AEF是由△AED翻折得到,
∴DE=EF,
∵DE+EC=DC,
∴EF+EC=DC,
故答案为EC.
②结论:△AFB∽△FEC.
理由:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠AFE=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠FEC=90°,
∴∠AFB=∠EFC,
∴△AFB∽△FEC.
(2)①如图2中,结论:FM=BM+CN.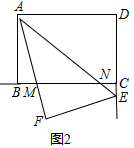
理由:∵△AEF是由△AED翻折得到,
∴∠DAE=∠EAF,AF=AD,
∵AD∥BC,AD=BC,
∴∠DAN=∠ANM,
∴∠MAN=∠MNA,
∴AM=MN,
∴FM+AM=AD=BC,
∴FM+MN=BC,
∵BM+CN+MN=BC,
∴FM=BM+CN.
②如图3中,结论:FM=CN-BM.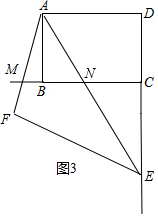
理由:易证FM+MN=BC,MN+CN-BM=BC,
所以FM=CN-BM.
点评 本题科学矩形的性质、翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是熟练掌握翻折不变性解决问题,所以中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | (2,4) | B. | (1,-3) | C. | (1,5) | D. | (-5,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
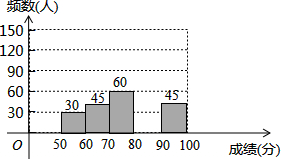 为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:| 组别 | 分数段 | 频数(人) | 频率 |
| 1 | 50≤x<60 | 30 | 0.1 |
| 2 | 60≤x<70 | 45 | 0.15 |
| 3 | 70≤x<80 | 60 | n |
| 4 | 80≤x<90 | m | 0.4 |
| 5 | 90≤x<100 | 45 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
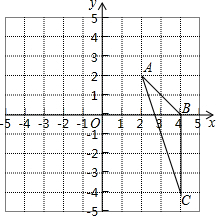 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com