
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 295 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
分析 (1)根据表中的数据,计算得出摸到白球的频率.
(2)由表中数据即可得;
(3)根据摸到白球的频率即可求出摸到白球概率.根据口袋中黑、白两种颜色的球的概率即可求出口袋中黑、白两种颜色的球有多少只.
解答 解:(1)完成表格如下:
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 295 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
点评 本题主要考查了如何利用频率估计概率,在解题时要注意频率和概率之间的关系,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
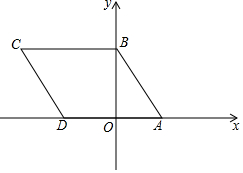 如图,边长为5的菱形ABCD如图所示放置在平面直角坐标系xOy中,点A在x轴正半轴上,点D在x轴负半轴上,点B(0,4).
如图,边长为5的菱形ABCD如图所示放置在平面直角坐标系xOy中,点A在x轴正半轴上,点D在x轴负半轴上,点B(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果线段AB和A′B′关于某条直线对称,那么AB=A′B′ | |
| B. | 如果点A和点A′到直线l的距离相等,A和A′关于直线l对称 | |
| C. | 如果AB=A′B′,且直线MN垂直平分AA′那么线段AB和A′B′关于直线MN对称 | |
| D. | 如果在直线MN两旁的两个图形能够完全重合,那么这两个图形关于直线MN对称 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
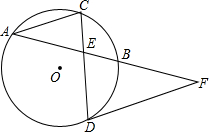 如图,⊙O的弦AB、CD相交于点E,C为$\widehat{AB}$的中点,过D点作⊙O的切线交AB的延长线于点F.
如图,⊙O的弦AB、CD相交于点E,C为$\widehat{AB}$的中点,过D点作⊙O的切线交AB的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com