
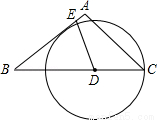
如图,在等腰△ABC中,AB=AC=5,BC=6,点D为BC边上一动点(不与点B重合),过D作射线DE交AB边于E,使∠BDE=∠A,以D为圆心、DC的长为半径作⊙D.
(1)设BD=x,AE=y,求y关于x的函数关系式,并写出定义域.
(2)当⊙D与AB边相切时,求BD的长.
(3)如果⊙E是以E为圆心,AE的长为半径的圆,那么当BD的长为多少时,⊙D与⊙E相切?
(1) y=5- x(0<x≤
x(0<x≤ );(2)
);(2)  ;(3)
;(3)  或
或 .
.
【解析】
试题分析:(1)通过相似三角形△BDE∽△BAC的对应边成比例得到 ,把相关线段的长度代入并整理得到y=5-
,把相关线段的长度代入并整理得到y=5- x(0<x≤
x(0<x≤ );
);
(2)如图,假设AB与⊙D相切于点F,连接FD.通过相似三角形△BFD∽△BGA的对应边成比例得到 .DF=6-BD,由勾股定理求得AG=4,BA=5,所以把相关线段的长度代入便可以求得BD的长度;
.DF=6-BD,由勾股定理求得AG=4,BA=5,所以把相关线段的长度代入便可以求得BD的长度;
(3)分类讨论:⊙D与⊙E相外切和内切两种情况.由(1)的相似三角形推知BD=ED.所以如图2,当⊙D与⊙E相外切时.AE+CD=DE=BD;如图3,当⊙D与⊙E相内切时.CD-AE=DE=BD.
试题解析:(1)如图,∵∠B=∠B,∠BDE=∠A,
∴△BDE∽△BAC,
∴ ,
,
∵AB=AC=5,BC=6,BD=x,AE=y,
∴ ,即y=5-
,即y=5- x.
x.
∵0<x≤6,且0≤y≤5,
∴0<x≤ .
.
综上所述,y关于x的函数关系式及其定义域为:y=5- x(0<x≤
x(0<x≤ );
);
(2)如图,假设AB与⊙D相切于点F,连接FD,则DF=DC,∠BFD=90°.
过点A作AG⊥BC于点G,则∠BGA=90°.
∴在△BFD和△BGA中,∠BFD=∠BGA=90°,∠B=∠B,
∴△BFD∽△BGA,
∴ .
.
又∵AB=AC=5,BC=6,AG⊥BC
∴BG= ,AG=
,AG= ,
,
∴ ,解得BD=
,解得BD= ;
;
(3)∵由(1)知,△BDE∽△BAC,
∴ ,即
,即 ,
,
∴BD=DE.
如图2,当⊙D与⊙E相外切时.
AE+CD=DE=BD,
∵由(1)知,BD=x,AE=y,y关于x的函数关系式是y=5- x,
x,
∴5- x+6-x=x,
x+6-x=x,
解得,x= ,符合0<x≤
,符合0<x≤ ,
,
∴BD的长度为 .
.
如图3,当⊙D与⊙E相内切时.CD-AE=DE=BD,
∵由(1)知,BD=x,AE=y,y关于x的函数关系式是y=5- x,
x,
∴6-x-5+ x=x,
x=x,
解得,x= ,符合0<x≤
,符合0<x≤ ,
,
∴BD的长度为 .
.
综上所述,BD的长度是 或
或 .
.



考点:圆的综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年上海市松江区中考二模数学试卷(解析版) 题型:选择题
已知一组数据x1,x2,x3的平均数和方差分别为6和2,则数据x1+1,x2+1,x3+1的平均数和方差分别是( )
A.6和2 B.6和3 C.7和2 D.7和3.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:填空题
从分别标有1、2、3、4的四张卡片中,一次同时抽2张,其中和为奇数的概率是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:选择题
下列图形既是中心对称又是轴对称的是( )
A.菱形 B.梯形 C.正三角形 D.正五边形
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:填空题
在平行四边形ABCD中,对角线AC,BD交于点O,设向量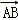 =
=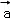 ,
,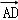 =
=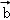 .用含
.用含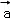 、
、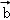 的式子表示向量
的式子表示向量 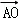 =
=
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市徐汇区中考二模数学试卷(解析版) 题型:解答题
如图,在△ABC中,AB=AC=10,sinC=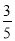 ,点D是BC上一点,且DC=AC.
,点D是BC上一点,且DC=AC.
(1)求BD的长;
(2)求tan∠BAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com