
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
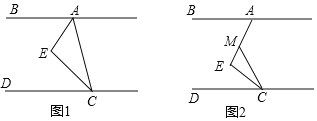
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
【答案】(1)AB∥CD.理由见解析;(2)∠BAE与∠MCD存在确定的数量关系:∠BAE+![]() ∠MCD=90°.
∠MCD=90°.
【解析】
(1)先根据CE平分∠ACD,AE平分∠BAC得出∠BAC=2∠EAC,∠ACD=2∠ACE,再由∠EAC+∠ACE=90°可知∠BAC+∠ACD=180°,故可得出结论;
(2)过E作EF∥AB,根据平行线的性质可知EF∥AB∥CD,∠BAE=∠AEF,∠FEC=∠DCE,故∠BAE+∠ECD=90°,再由∠MCE=∠ECD即可得出结论;
(1)AB∥CD.理由如下:
∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAE与∠MCD存在确定的数量关系:∠BAE+ ![]() ∠MCD=90°.
∠MCD=90°.
理由如下:
过E作EF∥AB,
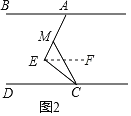
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE
∵∠E=90°,
∴∠BAE+∠ECD=90°
∵∠MCE=∠ECD,
∴∠BAE+ ![]() ∠MCD=90°.
∠MCD=90°.


科目:初中数学 来源: 题型:
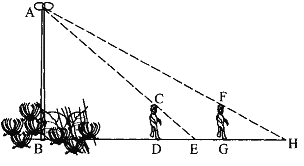
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
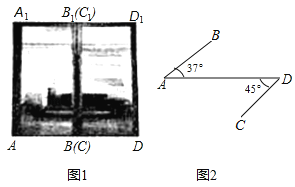
【题目】图1是一商场的推拉门,已知门的宽度![]() 米,且两扇门的大小相同(即
米,且两扇门的大小相同(即![]() ),将左边的门
),将左边的门![]() 绕门轴
绕门轴![]() 向里面旋转
向里面旋转![]() ,将右边的门
,将右边的门![]() 绕门轴
绕门轴![]() 向外面旋转
向外面旋转![]() ,其示意图如图2,求此时
,其示意图如图2,求此时![]() 与
与![]() 之间的距离(结果保留一位小数).(参考数据:
之间的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 中
中![]() 与
与![]() 交于
交于![]() 点,点
点,点![]() 在线段
在线段![]() 上,作直线
上,作直线![]() 交直线
交直线![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,设直线
,设直线![]() 交
交![]() 于
于![]() .
.

(1)如图,当![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() ;
;
(2)如图2,当![]() 在线段
在线段![]() 上,连接
上,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(3)在图3,当![]() 在线段
在线段![]() 上,连接
上,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足![]() ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
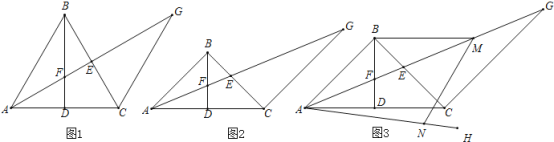
(1)如图1,若∠ABC=60°,求证:AF=![]() EG;
EG;
(2)如图2,若∠ABC=90°,求证:AF=![]() EG;
EG;
(3)在(2)的条件下如图3,过点A作∠CAH=![]() ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com