
【题目】如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
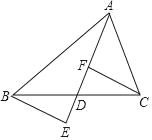
(1)求证:DE=DF;
(2)若在原有条件基础上再添加AB=AC,你还能得出什么结论.(不用证明)(写2个)
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,将△ABC在平面内绕点A逆时针旋转50角后得到△AB′C′的位置,若此时恰有CC′∥AB,则∠CAB′的度数为( )
A.15°
B.40°
C.50°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察图形,认真分析下列各式,然后解答问题.
OA![]() =(
=(![]() )2+1=2,S1=
)2+1=2,S1=![]() ;
;
OA![]() =(
=(![]() )2+1=3,S2=
)2+1=3,S2=![]() ;
;
OA![]() =(
=(![]() )2+1=4,S3=
)2+1=4,S3=![]() ;
;
…

求:(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S![]() +S
+S![]() +S
+S![]() +…+S
+…+S![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,已知1辆大货车与3辆小货车一次可以运货14吨,2辆大货车与5辆小货车一次可以运货25吨.
(1)1辆大货车与1辆小货车一次可以运货各多少吨?
(2)1辆大货车一次费用为300元,1辆小货车一次费用为200元,要求两种货车共用10辆,两次完成80吨的运货任务,且总费用不超过5400元,有哪几种用车方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知直线
中,已知直线 ![]() (
( ![]() )分别交反比例函数
)分别交反比例函数 ![]() 和
和 ![]() 在第一象限的图象于点
在第一象限的图象于点 ![]() ,
, ![]() ,过点
,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() ,交
,交 ![]() 的图象于点
的图象于点 ![]() ,连结
,连结 ![]() .若
.若 ![]() 是等腰三角形,则
是等腰三角形,则 ![]() 的值是 .
的值是 . 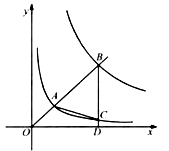
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题;△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度数可求.请回答:
(1)问题②中∠B的度数为 ;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=﹣1(a<b)的两根,则实数x1 , x2 , a,b的大小关系是( )
A.a<x1<x2<b
B.x1<a<x2<b
C.x1<a<b<x2
D.x1<x2<a<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路,甲队每天修建15米,乙队每天修建25米,一共用10天完成.
根据题意,小红和小芳同学分别列出了下面尚不完整的方程组:
小红:![]() 小芳:
小芳:
(1)请你分别写出小红和小芳所列方程组中未知数x,y表示的意义:
小红:x表示______,y表示______;
小芳:x表示______,y表示______;
(2)在题中“( )”内把小红和小芳所列方程组补充完整;
(3)甲工程队一共修建了______天,乙工程队一共修建了______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:

(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com