
【题目】阅读理解:对于任意正实数a、b,∵(![]() )2≥0,∴a-2
)2≥0,∴a-2![]() ,∴a+b≥2
,∴a+b≥2![]() ,当且仅当a=b时,等号成立.
,当且仅当a=b时,等号成立.
结论:在a+b![]() (a、b均为正实数)中,若ab为定值P,则a+b
(a、b均为正实数)中,若ab为定值P,则a+b![]() ,
,
当且仅当a=b时,a+b有最小值![]() .
.
根据上述内容,回答下列问题:
(1)若x>0,只有当x= 时,4x+![]() 有最小值为 .
有最小值为 .
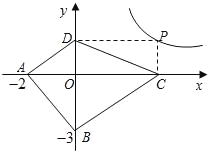
(2)探索应用:如图,已知A(-2,0),B(0,-3),点P为双曲线y=![]() (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D,求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D,求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(3)已知x>0,则自变量x为何值时,函数y=![]() 取到最大值,最大值为多少?
取到最大值,最大值为多少?
【答案】(1)![]() ,12;(2)最小值为12,四边形ABCD是菱形;(3)
,12;(2)最小值为12,四边形ABCD是菱形;(3)![]() .
.
【解析】
试题分析:(1)直接利用a+b≥2![]() ,当且仅当a=b时,等号成立;求解即可求得答案;
,当且仅当a=b时,等号成立;求解即可求得答案;
(2)首先设P(x,![]() ),则C(x,0),D(0,
),则C(x,0),D(0,![]() ),可得S四边形ABCD=
),可得S四边形ABCD=![]() ACBD=
ACBD=![]() (x+2)(
(x+2)(![]() +3),然后利用a+b≥2
+3),然后利用a+b≥2![]() ,当且仅当a=b时,等号成立求解即可求得答案;
,当且仅当a=b时,等号成立求解即可求得答案;
(3)首先将原式变形为y=![]() =
=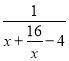 ,继而求得答案.
,继而求得答案.
试题解析:(1)∵4x+![]() ≥2×
≥2×![]() =12,当且仅当4x=
=12,当且仅当4x=![]() 时,等号成立,
时,等号成立,
∵x>0,
∴x=![]() ,
,
∴若x>0,只有当x=![]() 时,4x+
时,4x+![]() 有最小值为12;
有最小值为12;
(2)设P(x,![]() ),则C(x,0),D(0,
),则C(x,0),D(0,![]() ),
),
∴BD=![]() +3,AC=x+2,
+3,AC=x+2,
∴S四边形ABCD=![]() ACBD=
ACBD=![]() (x+2)(
(x+2)(![]() +3)=6+
+3)=6+![]() x+
x+![]() ≥6+2
≥6+2![]() =12,
=12,
当且仅当![]() x=
x=![]() ,即x=2时,四边形ABCD面积的最小值为12,
,即x=2时,四边形ABCD面积的最小值为12,
∴OB=OD=3,OA=OC=2,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
(3)∵x>0,
∴y=![]() =
=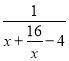 ≤
≤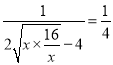 ,
,
当且仅当x=![]() ,即x=4时,函数y=
,即x=4时,函数y=![]() 取到最大值,最大值为:
取到最大值,最大值为:![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是( )
A. 先变长,后变短 B. 先变短,后变长
C. 方向改变,长短不变 D. 以上都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各命题是假命题的是( )
A.如果一个三角形的两个锐角互余,那么这个三角形是直角三角形
B.每个角都等于60°的三角形是等边三角形
C.如果a3=b3,那么a=b
D.对应角相等的三角形是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题是( )
A.等腰三角形两腰上的高相等
B.面积相等的两个三角形全等
C.两条直线被第三条直线所截,内错角相等
D.一个角的两边与另一个角的两边分别平行,那么这两个角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组线段中,能成比例的是( )
A. 1㎝,3㎝,4㎝,6㎝ B. 30㎝,12㎝,0.8㎝,0.2㎝
C. 0.1㎝,0.2㎝,0.3㎝,0.4㎝ D. 12㎝,16㎝,45㎝,60㎝
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com