
【题目】如图1,对称轴为直线x= ![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A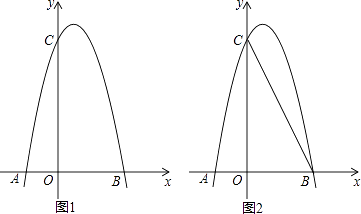
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:由对称性得:A(﹣1,0),
设抛物线的解析式为:y=a(x+1)(x﹣2),
把C(0,4)代入:4=﹣2a,
a=﹣2,
∴y=﹣2(x+1)(x﹣2),
∴抛物线的解析式为:y=﹣2x2+2x+4;
(2)解:如图1,设点P(m,﹣2m2+2m+4),过P作PD⊥x轴,垂足为D,

∴S=S梯形+S△PDB= ![]() m(﹣2m2+2m+4+4)+
m(﹣2m2+2m+4+4)+ ![]() (﹣2m2+2m+4)(2﹣m),
(﹣2m2+2m+4)(2﹣m),
S=﹣2m2+4m+4=﹣2(m﹣1)2+6,
∵﹣2<0,
∴S有最大值,则S大=6;
(3)解:存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形,
理由是:
分以下两种情况:
①当∠BQM=90°时,如图2:
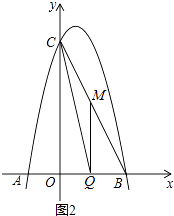
∵∠CMQ>90°,
∴只能CM=MQ.
设直线BC的解析式为:y=kx+b(k≠0),
把B(2,0)、C(0,4)代入得: ![]() ,
,
解得: ![]() ,
,
∴直线BC的解析式为:y=﹣2x+4,
设M(m,﹣2m+4),
则MQ=﹣2m+4,OQ=m,BQ=2﹣m,
在Rt△OBC中,BC= ![]() =
= ![]() =2
=2 ![]() ,
,
∵MQ∥OC,
∴△BMQ∽BCO,
∴ ![]() ,即
,即 ![]() ,
,
∴BM= ![]() (2﹣m)=2
(2﹣m)=2 ![]() ﹣
﹣ ![]() m,
m,
∴CM=BC﹣BM=2 ![]() ﹣(2
﹣(2 ![]() ﹣
﹣ ![]() m)=
m)= ![]() m,
m,
∵CM=MQ,
∴﹣2m+4= ![]() m,m=
m,m= ![]() =4
=4 ![]() ﹣8.
﹣8.
∴Q(4 ![]() ﹣8,0).
﹣8,0).
②当∠QMB=90°时,如图3,
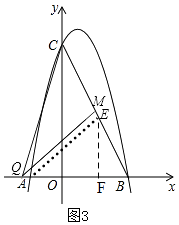
同理可设M(m,﹣2m+4),
过A作AE⊥BC,垂足为E,
∴∠EAB=∠OCB,
∴sin∠EAB= ![]() ,
,
∴ ![]() ,
,
∴BE= ![]() ,
,
过E作EF⊥x轴于F,
sin∠CBO= ![]() ,
,
∴ ![]() ,
,
∴EF= ![]() ,
,
由勾股定理得:BF= ![]() =
= ![]() ,
,
∴OF=2﹣ ![]() =
= ![]() ,
,
∴E( ![]() ,
, ![]() ),
),
由A(﹣1,0)和E( ![]() ,
, ![]() )可得:
)可得:
则AE的解析式为:y= ![]() x+
x+ ![]() ,
,
则直线BC与直线AE的交点E(1.4,1.2),
设Q(﹣x,0)(x>0),
∵AE∥QM,
∴△ABE∽△QBM,
∴ ![]() ①,
①,
由勾股定理得:x2+42=2×[m2+(﹣2m+4﹣4)2]②,
由以上两式得:m1=4(舍),m2= ![]() ,
,
当m= ![]() 时,x=
时,x= ![]() ,
,
∴Q(﹣ ![]() ,0).
,0).
综上所述,Q点坐标为(4 ![]() ﹣8,0)或(﹣
﹣8,0)或(﹣ ![]() ,0).
,0).
【解析】(1)首先依据点A与点B关于x=![]() 对称求得点A的坐标,然后利用待定系数法求求得抛物线的解析式即可;
对称求得点A的坐标,然后利用待定系数法求求得抛物线的解析式即可;
(2)设点P(m,﹣2m2+2m+4),过P作PD⊥x轴,垂足为D,然后得到S与m的函数关系式,接下来,依据二次函数的性质求得S的最大值即可;
(3)分为∠BQM=90°和∠QMB=90°两种情况画出图像,当∠BQM=90°时,先证明△BMQ∽BCO,然后再依据相似三角形的性质列方出求解即可;当∠QMB=90°时,过A作AE⊥BC,垂足为E,过E作EF⊥x轴于F,然后证明△ABE∽△QBM,然后再依据似三角形的性质列方出求解即可.


科目:初中数学 来源: 题型:
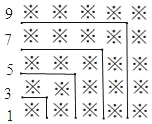
【题目】探索规律,观察下面由※组成的图案和算式,并解答问题.
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)试写出1+3+5+7+9+…+19= ;
(2)试写出1+3+5+7+9+…+(2n﹣1)= ;
(3)请用上述规律计算:
①101+103+105+107+…+2017+2019;
②(2m+1)+(2m+3)+(2m+5)+…+(2n+7)(其中n>m)(列出代数式即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若BC=2 ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣5),C(6,0)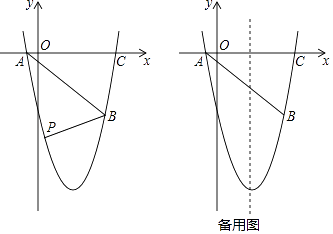
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)若点Q为抛物线的对称轴上的一个动点,试指出使△QAB为等腰三角形的点Q一共有几个?并请你求出其中一个点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面内有两点![]() 、
、![]() ,且
,且![]() 、
、![]() 两点之间的距离等于
两点之间的距离等于![]() (
(![]() 为大于0的已知数),在不计算
为大于0的已知数),在不计算![]() 的数值条件下,完成下列两题:
的数值条件下,完成下列两题:
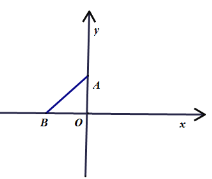
(1)以学过的知识用一句话说出![]() 的理由;
的理由;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形,如果存在,请写出点
是等腰三角形,如果存在,请写出点![]() 的坐标,并求
的坐标,并求![]() 的面积;如果不存在,请说明理由.
的面积;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
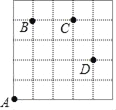
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com