
分析 采用反证法.假设存在一个十进制的质数$\overline{abc}$,使得b2-4ac为平方数.分别得到f(x)=ax2+bx+c=0①.已知条件意味着p=f(10)=a×102+b×10+c=$\overline{abc}$是一个质数方程①的两个根x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$②,取x=10,得p=a(10-x1)(10-x2)③.将式两边同乘以4a得 4ap=(20a-2ax1)(20a-2ax2)④.结合式④,导出|20a-2ax2|≤4a⑤.由式②推出式⑤不可能成立,矛盾,从而证明结论.
解答 证明:采用反证法.
假设存在一个十进制的质数$\overline{abc}$,使得b2-4ac为平方数.注意到求证结果的形式,可考虑(辅助的)二次方程
f(x)=ax2+bx+c=0①.
已知条件意味着 p=f(10)=a×102+b×10+c=$\overline{abc}$是一个质数.
由于b2-4ac是完全平方数,
故方程①的两个根x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$②
均为有理数.于是,
ax2+bx+c=a(x-x1)(x-x2).
取x=10,
得p=a(10-x1)(10-x2)③.
由式②可知2ax1、2ax2均是整数.
将式两边同乘以4a得 4ap=(20a-2ax1)(20a-2ax2)④.
因p是质数,所以,式④右边的两个因子中必有一个被p整除,不妨设20a-2ax1是p的倍数.
注意到20a-2ax1≠0,
故|20a-2ax1|≥p.
结合式④,导出|20a-2ax2|≤4a⑤.
但由式②易知x2≤0.
从而,式⑤不可能成立,矛盾.
点评 考查了完全平方数、质数与合数,当题目条件中出现形如b2-4ac一类平方与积的差的形式的式子时常利用判别式构造方程.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
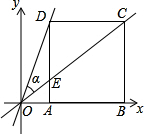 边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.
边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
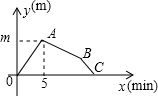 哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.
哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
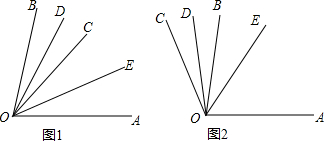 已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.
已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
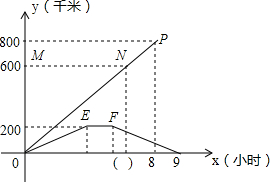 在笔直的公路上依次有A,B,C三地,甲车从A地出发速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地停留1小时后,按原速返回到C地,在两车行驶的过程中,甲、乙两车距各自出发的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
在笔直的公路上依次有A,B,C三地,甲车从A地出发速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地停留1小时后,按原速返回到C地,在两车行驶的过程中,甲、乙两车距各自出发的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两人分别从A、B两地同时出发,甲到达B地后立即原速返回A地,共用了20分钟,又过5分钟后乙也到达A地,如图为甲、乙两人距B地的路程y(米)与行使时间x(分钟)之间的函数图象.
甲、乙两人分别从A、B两地同时出发,甲到达B地后立即原速返回A地,共用了20分钟,又过5分钟后乙也到达A地,如图为甲、乙两人距B地的路程y(米)与行使时间x(分钟)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4a2+4a+1=(2a+1)2 | B. | a2-4b2=(a-4b)(a+b) | C. | a2-2a-1=(a-1)2 | D. | (a-b)(a+b)=a2-b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com