
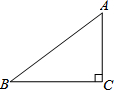
 如图,一张三角形纸片ABC,其中∠C=90°,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是m>n.
如图,一张三角形纸片ABC,其中∠C=90°,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是m>n. 分析 由三角形中位线定理求出m=4;由勾股定理求出AB=10,证明△BDF∽△BCA,得出对应边成比例求出DF即可.
解答 解: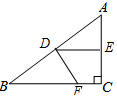 如图所示:
如图所示:
由折叠的性质得:DE是线段AC的垂直平分线,
∴DE是△ABC的中位线,
∴m=DE=$\frac{1}{2}$BC=4;
∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
由折叠的性质得:AD=BD=$\frac{1}{2}$AB=5,∠BDF=90°,
∵∠B=∠B,
∴△BDF∽△BCA,
∴$\frac{DF}{AC}=\frac{BD}{BC}$,即$\frac{DF}{6}=\frac{5}{8}$,
解得:DF=$\frac{15}{4}$,即n=$\frac{15}{4}$,
∴m>n;
故答案为:m>n.
点评 本题考查了折叠的性质、三角形中位线定理;,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.本题的关键是明确折痕是所折线段的垂直平分线,准确找出中位线,利用经过三角形一边中点与另一边平行的直线必平分第三边这一性质得出对应折痕的长,没有中位线的可以考虑用三角形相似来解决.


科目:初中数学 来源: 题型:填空题
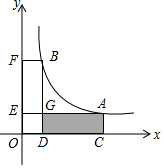 如图,A(a,b)、B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而增大.(填“减小”、“不变”或“增大”)
如图,A(a,b)、B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而增大.(填“减小”、“不变”或“增大”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
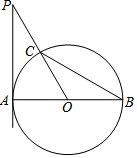 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,∠P=∠B.
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,∠P=∠B.查看答案和解析>>
科目:初中数学 来源:2017届山东省济宁市阶段教育学校统一招生考试数学模拟试卷(解析版) 题型:单选题
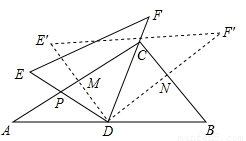
将一副三角尺(在RtΔABC中,∠ACB=90°,∠B=60°;在RtΔEDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将RtΔEDF绕点D顺时针方向旋转角α(0°<α<60°), DE?交AC于点M,DF?交BC于点N,则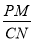 的值为( )
的值为( )
A. 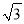 B.
B. 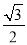 C.
C. 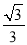 D.
D. 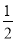
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省仙游县郊尾、枫亭五校教研小片区七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,已知AB∥CD,∠A=70°,则∠1度数是( )
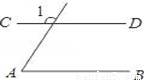
A. 70° B. 100° C. 110° D. 130°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com