
����Ŀ����ͼ1,��һ������������ABC�����ı�BC=60mm����AD=40mm��Ҫ�����ӹ��������������ʹ�����ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ��ʼӹ��ɵ�����������ı߳��Ƕ���mm��������㡣
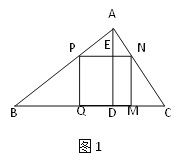
��ʽ��1�����ԭ����Ҫ�ӹ��������һ�����Σ��Ҵ˾��������������ŷ��õ�����������ɣ���ͼ2����ʱ�������������������߳��ֱַ�Ϊ����mm��������㣮
��ʽ��2�����ԭ������Ҫ�ӹ������ֻ��һ�����Σ���ͼ3���������˾�������������߳��Ͳ���ȷ���������������������ֵ����ﵽ������ֵʱ��������������߳���

���𰸡���1�������������������߳��ֱ�Ϊ![]() mm��
mm��![]() mm��
mm��
��2��S�����ֵʱ��PN=30mm��PQ=20mm.
�������������������1���������εı߳�Ϊxmm����PN=PQ=ED=x��AE=AD-ED=80-x��ͨ��֤����APN�ס�ABC���������Ʊȿɵõ�![]() ��Ȼ����ݱ����������x���ɣ�
��Ȼ����ݱ����������x���ɣ�
��2�����ھ��������������ŷ��õ�����������ɣ������PQ=x����PN=2x��AE=40-x��Ȼ���루1���ķ���һ����⣻��3����PN=x����PQ��ʾ��AE�ij��ȣ�Ȼ��������������ζ�Ӧ�ߵıȵ������Ʊ��г�����ʽ����x��ʾ��PN��Ȼ����ݾ��ε������ʽ��ʽ���㣬�ٸ��ݶ��κ�������ֵ������
�����������1����ͼ1���������εı߳�Ϊxmm����PN=PQ=ED=x����AE=ADED=40x����PN��BC��
���APN�ס�ABC��
��![]() ,��
,��![]() ��
��
���x=24.
��ӹ��ɵ�����������ı߳���24mm��
(2)��ͼ2����PQ=x����PN=2x��AE=40x��
��PN��BC��
���APN�ס�ABC��
��![]() ,��
,��![]() ��
��
��ã�x=![]() ��
��
��2x=![]() ,
,
�������������������߳��ֱ�Ϊ![]() mm,
mm, ![]() mm��
mm��
(3)��ͼ3,��PN=x(mm),����PQMN�����ΪS(mm2)��
�������ɵá�APN�ס�ABC��
��![]() ,��
,��![]() ��
��
��ã�PQ=![]() .
.
��S=PNPQ=x(![]() )=
)=![]() x2+40x=
x2+40x=![]() (x30)2+600��
(x30)2+600��
��S�����ֵΪ600mm2,��ʱPN=30mm,PQ=40![]() ��30=20(mm).
��30=20(mm).


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��F��C��E��ֱ��l����F��C֮�䲻��ֱ�Ӳ���������A��D��l��࣬���AB=DE��AC=DF��BF=EC.
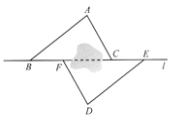
��1����֤����ABC�ա�DEF��
��2��ָ��ͼ������ƽ�е��߶Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ���E��BC���ӳ����ϣ���CE=BC��AE=AB��AE��DC�ཻ�ڵ�O������DE��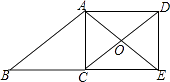
��1����֤���ı���ACED�Ǿ��Σ�
��2������AOD=120�㣬AC=4����Խ���CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3cm������P��B�������3cm/s���ٶ����ű�BC��CD��DA�˶�������A��ֹͣ�˶�����һ����Qͬʱ��B���������1cm/s���ٶ����ű�BA��A���˶�������A��ֹͣ�˶�����P���˶�ʱ��Ϊx��s������BPQ�����Ϊy��cm2������y����x�ĺ���ͼ���ǣ�������
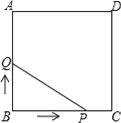
A. 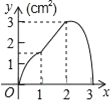 B.
B. 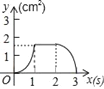 C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ���ı���ABCD�У�AB=5��AEƽ�֡�DAB��BC����ֱ���ڵ�E��CE=2����AD= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ρ��ȱ������Ρ����Ρ������κ�Բ�����ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�εĸ�����__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �������ݣ�75��80��85��85��85�����������ݵ���������λ���ǣ�������
A.75��80B.85��85C.80��85D.80��75
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������г�����֦�ļ۸��ȥ�������5%��ȥ��ļ۸���ÿǧ��mԪ�������ļ۸���ÿǧ��Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com