
【题目】解方程:
(1) ![]() ;
;
(2) ![]() (用配方法);
(用配方法);
(3) ![]()
(4) ![]()
【答案】(1) ![]() ; (2)
; (2) ![]() ;(3)
;(3) ![]() ;(4)
;(4)![]() .
.
【解析】试题分析:(1)移项后两边开方,求出方程的解即可;
(2)把常数项1移项后,应该在左右两边同时加上一次项系数-5的一半的平方;
(3)利用配方法解方程;
(4)设t=x-2,原方程转化为9t2-6t+1=0,通过解该方程求得t的值;然后代入来求x的值.
解:(1)(x5)29=0,
(x5)2=9,
x5=±3,
x1=8,x2=2;
(2)x25x+1=0,
x25x=1
x25x+![]() =1+
=1+![]() ,
,
(x![]() )2=
)2=![]()
x1=![]() ,x2=
,x2=![]() ;
;
(3)3y21=6y,
y22y+1=![]() +1,
+1,
(y1)2=![]() ,
,
y1=±![]() ,
,
y1=![]() ,y2=
,y2=![]() ;
;
(4)设t=x2,原方程转化为9t26t+1=0,
整理,得
(3t1)2=0,
解得t=![]() ,
,
所以x2=![]() ,
,
则x1=x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点B、C为线段AD上的两点,AB=![]() BC=
BC=![]() CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
如图1,⊙O1和⊙O2外切于点C,AB是⊙O1和⊙O2外公切线,A、B为切点,
求证:AC⊥BC
证明:过点C作⊙O1和⊙O2的内公切线交AB于D,
∵DA、DC是⊙O1的切线
∴DA=DC.
∴∠DAC=∠DCA.
同理∠DCB=∠DBC.
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°,
∴∠DCA+∠DCB=90°.
即AC⊥BC.
根据上述材料,解答下列问题:
(1)在以上的证明过程中使用了哪些定理?请写出两个定理的名称或内容;
(2)以AB所在直线为x轴,过点C且垂直于AB的直线为y轴建立直角坐标系(如图2),已知A、B两点的坐标为(﹣4,0),(1,0),求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式;
(3)根据(2)中所确定的抛物线,试判断这条抛物线的顶点是否落在两圆的连心O1O2上,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() ,
,![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() .
.
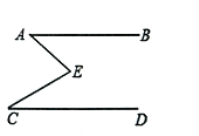
(1)问题发现:
①若![]() ,
,![]() ,则
,则![]() .
.
②猜想图![]() 中
中![]() 、
、![]() 、
、![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
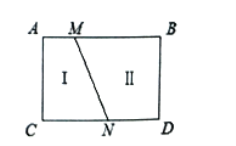
(2)拓展应用:
如图![]() ,
,![]() ,线段
,线段![]() 把
把![]() 这个封闭区域分为
这个封闭区域分为![]() 、
、![]() 两部分(不含边界),点
两部分(不含边界),点![]() 是位于这两个区域内的任意一点(不在边界上),请直接写出
是位于这两个区域内的任意一点(不在边界上),请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
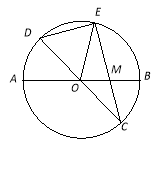
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=![]() .
.
(1)求证:![]() ;
;
(2)求EM的长;
(3)求sin∠EOB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com