
已知﹣2xm﹣2y2与3x4y2m+n是同类项,则m﹣3n的平方根是_____.
±6 【解析】试题分析:同类项是指所含字母相同,且相同字母的指数也相同的两个单项式,根据定义可知: ,解得: ,则m-3n=6+30=36,则m-3n的平方根为: .科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
(1)详见解析;(2). 【解析】试题分析:(1)由旋转的性质可知,DE=DM,∠EDM=90°,因为∠EDF=45°,所以∠FDM=∠EDM=45°,通过证明△DEF≌△DMF得到EF=MF; (2)设EF=MF=x,则BF=4-x,BE=2,在Rt△EBF中,由勾股定理得到关于x的等式,解得x的值即可. 试题解析:(1)证明:∵△DAE逆时针旋转90°得到△DCM, ∴...查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:单选题
顺次连接任意四边形四边中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
A 【解析】 试题分析:顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形. 【解析】 连接BD, 已知任意四边形ABCD,E、F、G、H分别是各边中点. ∵在△ABD中,E、H是AB、AD中点, ∴EH∥BD,EH=BD. ∵在△BCD中,G、F是DC、BC中点, ...查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型:单选题
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )

A.二次函数图像与x轴交点有两个
B.x≥2时y随x的增大而增大
C.二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D.对称轴为直线x=1.5
D 【解析】 试题分析:根据题目提供的满足二次函数解析式的x、y的值,确定二次函数的对称轴,利用对称轴找到一个点的对称点的纵坐标即可. 【解析】 由上表可知函数图象经过点和点,, ∴a=1,b=-2, 对称轴为, 故答案为:D.查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:解答题
在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画出所有符合条件的整点三角形.
(1)在图1中画△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.

查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:填空题
计算:(﹣ )﹣2+(﹣2017)0=_____.
)﹣2+(﹣2017)0=_____.
查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
在平面直角坐标系中,点P(﹣1,2)的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B 【解析】 试题分析:本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).∵点P(﹣1,2)的横坐标﹣1<0,纵坐标2>0,∴点P在第二象限.查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:填空题
一个底面直径是80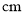 ,母线长为
,母线长为 的圆锥的侧面展开图的圆心角的度数为______ 。
的圆锥的侧面展开图的圆心角的度数为______ 。
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,某塔观光层的最外沿点E为蹦极项目的起跳点,已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据 ≈1.4,
≈1.4, 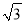 ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com