

 解:(1)∵四边形ABCD为等腰梯形,
解:(1)∵四边形ABCD为等腰梯形,

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
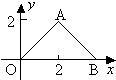 (2005•湘潭)如图,在△AOB中,AO=AB,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′、B′在x轴上.则点B'的坐标是
(2005•湘潭)如图,在△AOB中,AO=AB,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′、B′在x轴上.则点B'的坐标是查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《三角形》(10)(解析版) 题型:解答题
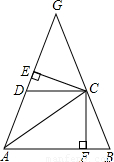
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《三角形》(07)(解析版) 题型:填空题
 上一点,则∠ACB= 度.
上一点,则∠ACB= 度.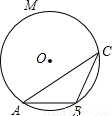
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《一元一次方程》(01)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2005年湖南省湘潭市中考数学试卷(大纲卷)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com