
【题目】将一副三角板按如图方法摆放在一起,连接AC,则tan∠DAC值为( )

A.1 B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
试题分析:先过点C作CE⊥AD于E,设CD=a,在Rt△BDC中,利用三角函数,可求BD,在Rt△DBA中,利用三角函数,可求AD,易证△CED是等腰直角三角形,从而利用三角函数可求CE、DE,于是在Rt△CAE中,可求tan∠EAC=![]() =
=![]() ,即tan∠DAC的值.
,即tan∠DAC的值.
解:如图所示,过点C作CE⊥AD于E,
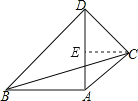
设CD=a,
在Rt△BDC中,∠DBC=30°,则
BD=cot30°×CD=![]() a,
a,
在Rt△DBA中,AD=sin45°×BD=![]() a,
a,
又∵CE⊥AD,∠BDA=45°,
∴DE=CE=sin45°×a=![]() a,
a,
∴在Rt△CAE中,tan∠EAC=![]() =
=![]() =
=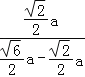 =
=![]() .
.
即tan∠DAC=![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0
(1)求证:无论k为任何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且|x1﹣x2|=2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6![]() 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程适合用求根公式法解的是( )
A. (x﹣3)2=2 B. 325x2﹣326x+1=0
C. x2﹣100x+2500=0 D. 2x2+3x﹣1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球绕太阳每小时转动经过的路程约为110000米,将110000用科学记数法表示为( )
A. 11×104 B. 0.11×107 C. 1.1×106 D. 1.1×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程2x2+px+q=0的两个根为3,4,那么因式分解二次三项式2x2+px+q=( )
A. (x﹣3)(x﹣4) B. (x+3)(x+4) C. 2(x﹣3)(x﹣4) D. 2(x+3)(x+4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com