
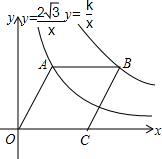
 如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$.
如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$. 分析 首先根据点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,设A点坐标为(a,$\frac{2\sqrt{3}}{a}$),再利用含30°直角三角形的性质算出OA=2a,再利用菱形的性质进而得到B点坐标,即可求出k的值.
解答 解:因为点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,设A点坐标为(a,$\frac{2\sqrt{3}}{a}$),
因为四边形OABC是菱形,且∠AOC=60°,
所以OA=2a,
可得B点坐标为(3a,$\frac{2\sqrt{3}}{a}$),
可得:k=$3a×\frac{2\sqrt{3}}{a}=6\sqrt{3}$,
故答案为:$6\sqrt{3}$
点评 此题主要考查了待定系数法求反比例函数,关键是根据菱形的性质求出B点坐标,即可算出反比例函数解析式.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
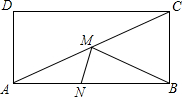 如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )| A. | 10 | B. | 8 | C. | 5$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
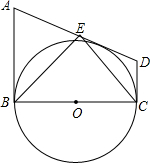 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 1 | 2 | 4 | 5 | … |
| y1 | … | -5 | 0 | 4 | 3 | -5 | -12 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
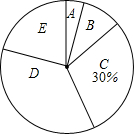 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 2 |
| B | 41≤x<46 | 5 |
| C | 46≤x<51 | 15 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
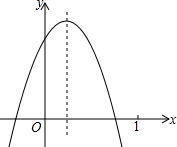 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
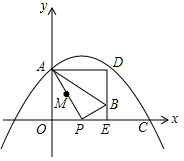 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com