
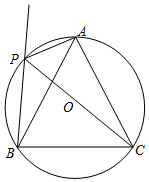
 如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.
如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.分析 (1)根据等边三角形的性质得∠ABC=∠BAC=60°,再根据圆周角定理得∠APB=∠ABC=60°,∠BPC=∠BAC=60°,所以∠APC=∠BPC;
(2)首先在线段PC上截取PF=PB,连接BF,进而得出△BPA≌△BFC(AAS),即可得出PA+PB=PF+FC=PC;
(3)先证明△ADP∽△CAP,根据相似的性质得PD:PA=PA:PC,即PD:2=2:5,可计算出PD=$\frac{4}{5}$,再证明△ADP∽△BDA,由相似比得到AD:DP=DB:DA=AB:PA,计算出AD=$\frac{2\sqrt{19}}{5}$,AB=$\frac{5}{2}$AD=$\sqrt{19}$,即得到等边三角形的边长,接着求得等边三角形的高,即可求得面积.
解答 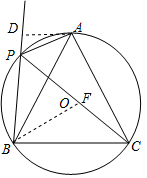 (1)证明:∵△ABC为等边三角形,
(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
∵∠APB=∠ABC=60°,∠BPC=∠BAC=60°,
∴∠APC=∠BPC,
∴PC平分∠APB;
(2)解:PA+PB=PC,
证明:在线段PC上截取PF=PB,连接BF,
∵PF=PB,∠BPC=60°,
∴△PBF是等边三角形,
∴PB=BF,∠BFP=60°,
∴∠BFC=180°-∠PFB=120°,
∵∠BPA=∠APC+∠BPC=120°,
∴∠BPA=∠BFC,
在△BPA和△BFC中,
$\left\{\begin{array}{l}{∠PAB=∠BCF}\\{∠APB=∠BFC}\\{BP=BF}\end{array}\right.$,
∴△BPA≌△BFC(AAS),
∴PA=FC,
∴PA+PB=PF+FC=PC;
(3)过A点作⊙O的切线交直线PB于D,
∴∠DAP=∠ACP,∠DAB=∠ACB=60°,
而∠APD=∠ACB=60°,∠ABD=∠ACP,
∴∠APD=∠APC=∠BAD=60°,∠PAD=∠ABD,
∴△ADP∽△CAP,
∴PD:PA=PA:PC,即PD:2=2:5,
∴PD=$\frac{4}{5}$,
∵BP=PC-PA=5-2=3,
∵BD-PB=PD,
∴BD=$\frac{4}{5}$+3=$\frac{19}{5}$,
∵∠APD=∠BAD,∠PAD=∠ABD,
∴△ADP∽△BDA,
∴AD:DP=DB:DA=AB:PA,
∴$\frac{AD}{\frac{4}{5}}$=$\frac{\frac{19}{5}}{AD}$=$\frac{AB}{2}$
∴AD=$\frac{2\sqrt{19}}{5}$,AB=$\frac{5}{2}$AD=$\sqrt{19}$,
∴△ABC的高=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{57}}{2}$,
∴△ABC的面积为:$\frac{1}{2}$×$\sqrt{19}$×$\frac{\sqrt{57}}{2}$=$\frac{19\sqrt{3}}{4}$.
点评 此题主要考查了相似三角形的判定与性质以及全等三角形的判定与性质和切线的性质等知识,能够熟练运用相似三角形的判定与性质是解题关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
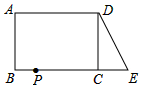 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为1或7秒时,△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为1或7秒时,△ABP和△DCE全等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com