
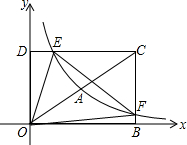
 如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.分析 (1)先利用矩形的性质确定C点坐标(3,2),再确定A点坐标为($\frac{3}{2}$,1),则根据反比例函数图象上点的坐标特征得到k1=3,即反比例函数解析式为y=$\frac{3}{x}$;然后利用反比例函数解析式确定F点的坐标为(3,$\frac{1}{2}$),E点坐标为($\frac{3}{4}$,2),再利用待定系数法求直线EF的解析式;
(2)利用△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF进行计算;
(3)观察函数图象得到当$\frac{3}{4}$<x<3时,一次函数图象都在反比例函数图象上方,即k2x+b>$\frac{{k}_{1}}{x}$.
解答 解:(1)∵四边形DOBC是矩形,且D(0,2),B(3,0),
∴C点坐标为(3,2),
∵点A为线段OC的中点,
∴A点坐标为($\frac{3}{2}$,1),
∴k1=$\frac{3}{2}$×1=$\frac{3}{2}$,
∴反比例函数解析式为y=$\frac{3}{2x}$;
把x=3代入y=$\frac{3}{2x}$,得y=$\frac{1}{2}$,则F点的坐标为(3,$\frac{1}{2}$);
把y=2代入y=$\frac{3}{2x}$得x=$\frac{3}{4}$,则E点坐标为($\frac{3}{4}$,2),
把F(3,$\frac{1}{2}$)、E($\frac{3}{4}$,2)代入y=k2x+b得$\left\{\begin{array}{l}{3{k}_{2}+b=\frac{1}{2}}\\{\frac{3}{4}{k}_{2}+b=2}\end{array}\right.$,解得--$\left\{\begin{array}{l}{{k}_{2}=-\frac{2}{3}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴直线EF的解析式为y=-$\frac{2}{3}$x+$\frac{5}{2}$;
(2)△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF
=2×3-$\frac{1}{2}$×2×$\frac{3}{4}$-$\frac{1}{2}$×3×$\frac{1}{2}$-$\frac{1}{2}$×(3-$\frac{3}{4}$)×(2-$\frac{1}{2}$)
=$\frac{45}{16}$;
(3)由图象得:不等式k2x+b-$\frac{{k}_{1}}{x}$>0的解集为$\frac{3}{4}$<x<3.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法确定函数解析式.


科目:初中数学 来源: 题型:解答题
| 类型 | A | B |
| 单瓶饮料体积/升 | 1 | 2.5 |
| 单价/元 | 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
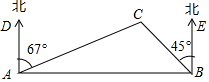 一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).
一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
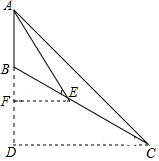 如图,测量人员计划测量山坡上一信号塔的高度,测量人员在山脚C处,测得塔顶A的仰角为45°,测量人员沿着坡度i=1:$\sqrt{3}$的山坡BC向上行走100米到达E处,再测得塔顶A的仰角为53°,则山坡的高度BD约为(精确到0.1米,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈4/3,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)( )
如图,测量人员计划测量山坡上一信号塔的高度,测量人员在山脚C处,测得塔顶A的仰角为45°,测量人员沿着坡度i=1:$\sqrt{3}$的山坡BC向上行走100米到达E处,再测得塔顶A的仰角为53°,则山坡的高度BD约为(精确到0.1米,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈4/3,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)( )| A. | 100.5米 | B. | 110.5米 | C. | 113.5米 | D. | 116.5米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3或-1 | B. | -3或-1 | C. | -3或1 | D. | 3或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
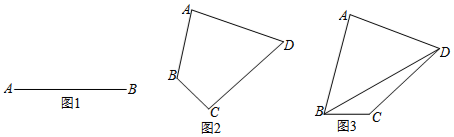
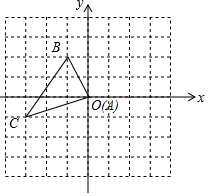 在边长为1的正方形网格中建立平面直角坐标系,△ABC位置如图.
在边长为1的正方形网格中建立平面直角坐标系,△ABC位置如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
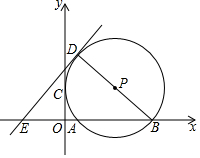 如图,已知⊙P与x轴交于A和B(9,0)两点,与y轴的正半轴相切与点C(0,3),作⊙P的直径BD,过点D作直线DE⊥BD,交x轴于E点,若点P在双曲线y=$\frac{15}{x}$上,则直线DE的解析式为y=$\frac{12}{7}$x+$\frac{30}{7}$.
如图,已知⊙P与x轴交于A和B(9,0)两点,与y轴的正半轴相切与点C(0,3),作⊙P的直径BD,过点D作直线DE⊥BD,交x轴于E点,若点P在双曲线y=$\frac{15}{x}$上,则直线DE的解析式为y=$\frac{12}{7}$x+$\frac{30}{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com