
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)方程移项得:5x-3x=9+3,
合并同类项得:2x=12,
解得:x=6;
(2)去分母,得3(3x-7)-2(1+x)=6,
去括号,得9x-21-2-2x=6,
移项、合并同类项,得7x=29,
系数化为1,得x=$\frac{29}{7}$;
(3)去分母得:6+3(x-1)=x+2,
去括号得:6+3x-3=x+2,
移项合并得:2x=-1,
解得:x=-0.5.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 如图,已知长方形ABCD,E为BC边上的一点,现将△ABE沿AE翻折,翻折后点B恰好落在边DC上点F处.
如图,已知长方形ABCD,E为BC边上的一点,现将△ABE沿AE翻折,翻折后点B恰好落在边DC上点F处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5cm | B. | 6cm | C. | $\sqrt{5}$cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
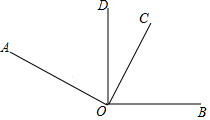 如图,已知∠AOB=155°,∠AOC=∠BOD=90°.
如图,已知∠AOB=155°,∠AOC=∠BOD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0不是单项式 | B. | -$\frac{abc}{2}$的系数是$-\frac{1}{2}$ | ||
| C. | -23a2b3c的次数是8 | D. | x2y的系数是0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
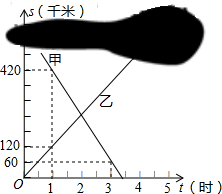 甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.
甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com