
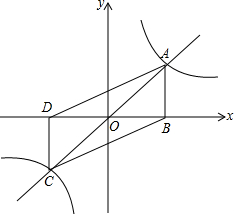
 如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,求证:当k取不同正数时,四边形ABCD的面积是常数.
如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,求证:当k取不同正数时,四边形ABCD的面积是常数. 分析 根据正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,以及正比例函数与反比例函数的交点关于原点对称,从而可以设出点A的坐标,从而可以得到点B、C、D的坐标,从而可以求出组成四边形ABCD的各三角形的面积,再根据反比例函数可得到四边形的面积的值,从而可以解答本题.
解答 证明:∵正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,
∴设点A的坐标为(x,y),则点B的坐标为(x,0)点C的坐标为(-x,-y),点D的坐标为(-x,0).
∴S△OAB+S△OBC+S△OCD+S△ODA=$\frac{xy}{2}+\frac{x×|-y|}{2}+\frac{|-x||-y|}{2}+\frac{|-x|y}{2}$=$\frac{xy}{2}+\frac{xy}{2}+\frac{xy}{2}+\frac{xy}{2}=2xy$.
∵点A在$y=\frac{1}{x}$上,
∴xy=1.
∵S四边形ABCD=S△OAB+S△OBC+S△OCD+S△ODA=2xy,
∴S四边形ABCD=2.
即当k取不同正数时,四边形ABCD的面积是常数.
点评 本题考查反比例函数与正比例函数的交点问题,解题的关键是明确它们的交点之间的关系,能将四边形的面积转化为求组成它的三角形的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
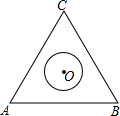 如图,等边△ABC中,AB=4$\sqrt{3}$,O为三角形中心,⊙O的直径为1,现将⊙O沿某一方向平移,当它与等边△ABC的某条边相切时停止平移,记平移的距离为d,则d的取值范围是1≤d≤2.
如图,等边△ABC中,AB=4$\sqrt{3}$,O为三角形中心,⊙O的直径为1,现将⊙O沿某一方向平移,当它与等边△ABC的某条边相切时停止平移,记平移的距离为d,则d的取值范围是1≤d≤2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com