
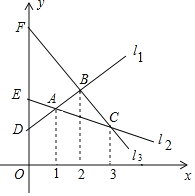
【题目】如图,l1、l2、l3两两相交于A、B、C三点,它们与y轴正半轴分别交于点D、E、F,若A、B、C三点的坐标分别为(1,yA)、(2,yB)、(3,yC),且OD=DE=1,则下列结论正确的个数是( )①EC=3EA,②S△ABC=1,③OF=5,④2yA﹣yA﹣yC=2
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①如图,由平行线等分线段定理(或分线段成比例定理)易得:![]() ;
;
②设过点B且与y轴平行的直线交AC于点G,则S△ABC=S△AGB+S△BCG,易得:S△AED=![]() ,△AED∽△AGB且相似比=1,所以,△AED≌△AGB,所以,S△ABG=S△BCG=
,△AED∽△AGB且相似比=1,所以,△AED≌△AGB,所以,S△ABG=S△BCG=![]() ,又易得G为AC中点,所以,S△AGB=S△BGC=
,又易得G为AC中点,所以,S△AGB=S△BGC=![]() ,从而得结论;
,从而得结论;
③易知,BG=DE=1,又△BGC∽△FEC,列比例式可得结论;
④易知,点B的位置会随着点A在直线x=1上的位置变化而相应的发生变化,所以④错误.
①如图,∵OE∥AA'∥CC',且OA'=1,OC'=3,
∴![]() ,
,
∴EC=3EA,
故 ①正确;
②设过点B且与y轴平行的直线交AC于点G(如图),则S△ABC=S△AGB+S△BCG,
∵DE=1,OA'=1,
∴S△AED= ![]() ,
,
∵OE∥AA'∥GB',OA'=A'B',
∴AE=AG,
∴△AED∽△AGB且相似比=1,
∴△AED≌△AGB,
∴S△ABG= ![]() ,
,
同理得:G为AC中点,
∴S△ABG=S△BCG=![]() ,
,
∴S△ABC=1,
故 ②正确;
③由②知:△AED≌△AGB,
∴BG=DE=1,
∵BG∥EF,
∴△BGC∽△FEC,
∴![]() ,
,
∴EF=3.即OF=5,
故③正确;
④易知,点B的位置会随着点A在直线x=1上的位置变化而相应的发生变化,
故④错误;
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A,B两点,交x轴于D,C两点,连接
交于A,B两点,交x轴于D,C两点,连接![]() ,
,![]() ,已知
,已知![]() ,
,![]() .
.
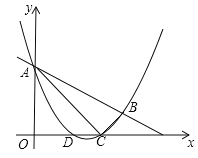
(1)求抛物线的解析式;
(2)P为y轴右侧抛物线上一动点,连接![]() ,过点P作
,过点P作![]() 交y轴于点Q,问:是否存在点P使得以A,P,Q为项点的三角形与
交y轴于点Q,问:是否存在点P使得以A,P,Q为项点的三角形与![]() 相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)设E为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点M从点D出发,沿线段
,一动点M从点D出发,沿线段![]() 以每秒一个单位速度运动到E点,再沿线段
以每秒一个单位速度运动到E点,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
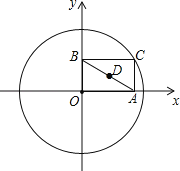
【题目】如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是AB的中点,如果点C在圆上运动一周,那么点D运动过的路程长为( )
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
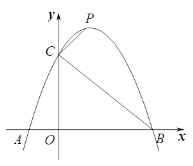
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
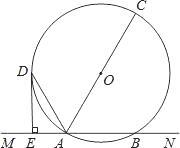
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长交过点A的切线于点G,且满足AG∥BC,连接OC,若cos∠BAC=![]() ,BC=6.
,BC=6.
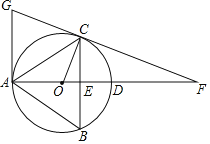
(1)求证:∠COD=∠BAC;
(2)求⊙O的半径OC;
(3)求证:CF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是( )
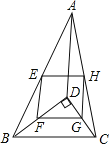
A.24B.20C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.

(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=24cm,水面最深地方的高度为8cm,求这个圆形截面的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com