
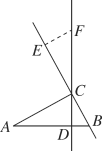
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)当点E运动多长时间时,CF=AB.请说明理由.
【答案】(1)详见解析;(2)当点E运动5s或2s时,CF=AB.
【解析】
(1)根据余角的性质即可得到结论;(2)如图,当点E在射线BC上移动时,若E移动5s,则BE=2×5=10cm,根据全等三角形的判定和性质即可得到结论.
(1)∵∠ACB=90°,CD⊥AB,∴∠A+∠ACD=90°,∠BCD+∠ACD=90°,∴∠A=∠BCD.
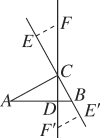
(2)如图,当点E在射线BC上移动5s时,CF=AB.可知BE=2×5=10(cm),∴CE=BE-BC=10-3=7(cm),∴CE=AC.∵∠A=∠BCD,∠ECF=∠BCD,∴∠A=∠ECF.(5分)在△CFE与△ABC中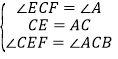 ,
,
∴△CFE≌△ABC,∴CF=AB.(7分)当点E在射线CB上移动2s时,CF=AB.可知BE′=2×2=4(cm),∴CE′=BE′+BC=4+3=7(cm),∴CE′=AC.在△CF′E′与△ABC中
∴△CF′E′≌△ABC,∴CF′=AB.
综上可知,当点E运动5s或2s时,CF=AB.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某公园门票价是每人10元,公园规定:如果一次购票满30张,每张可少收2元.
(1)若某班有18名同学去公园,则需要 元;
(2)若某班有![]() 名同学去公园共需要 元;
名同学去公园共需要 元;
(3)若某班有27名同学去公园,怎样买票更合算?最少需要多少元?
(4)若某班去公园共交费240元,则该班可能有多少人去公园?
查看答案和解析>>
科目:初中数学 来源: 题型:
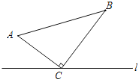
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.
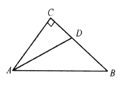
(1)若BC=7,BD=4,则点![]() 到
到![]() 的距离是________;
的距离是________;
(2)若![]() ,点
,点![]() 到
到![]() 的距离是8,则
的距离是8,则![]() 的长是________.
的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ]= ;[
]= ;[![]() ]= .
]= .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
(3)如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次[![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.对145连续求根整数, 次之后结果为1.
]=1,这时候结果为1.对145连续求根整数, 次之后结果为1.
查看答案和解析>>
科目:初中数学 来源: 题型:
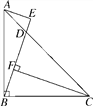
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
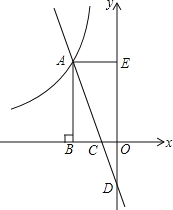
【题目】如图,直线y=kx﹣2与双曲线y=-![]() (x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E, △ABC的面积为2.
(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E, △ABC的面积为2.
(1)直接写出四边形OCAE的面积;
(2)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车站相距![]() ,一列慢车从甲站开出,每小时行驶
,一列慢车从甲站开出,每小时行驶![]() ,一列快车从乙站开出,每小时行驶
,一列快车从乙站开出,每小时行驶![]() .(必须用方程解,方程以外的方法不计分)
.(必须用方程解,方程以外的方法不计分)
(1)两车同时开出,相向而行,多少小时相遇?
(2)两车同时开出,同向而行,慢车在前,多少小时快车追上慢车?
查看答案和解析>>
科目:初中数学 来源: 题型:
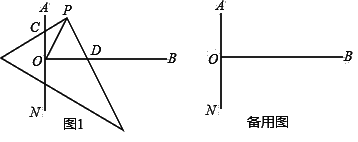
【题目】如图1,射线OB与直线AN垂直于点O,线段OP在∠AOB内,一块三角板的直角顶点与点P重合,两条直角边分别与AN、OB的交于点C、D.
(1)当∠POB=60°,∠OPC=30°,PC=2时,则PD= .
(2)若∠POB=45°,
①当PC与PO重合时,PC和PD之间的数量关系是 ;
②当PC与PO不重合时,猜想PC与PD之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com