Question

5．如图1，平行四边形ABCD的一边DC向右匀速平行移动，图2反映它的底边BC的长度l（cm）所时间t（s）变化而变化的情况．
问：（1）这个变化过程中，自变量、因变量各式什么？
（2）DC边没有运动时，底边BC长度是多少？
（3）DC边向右运动了多长时间？
（4）观察图3，在图2的基础上推测DC边在5s后的运动情况是怎样的？
（5）图4反映了变化过程中平行四边形ABCD的面积S（cm²）随时间t（s）变化的情况．
①平行四边形ABCD中，BC边上的高为2cm；
②当t=2s时，面积S的值为24cm²，当t=12s时，面积S的值为12cm²，说一说，S值是怎样随t值的变而变化的？

Answer 1

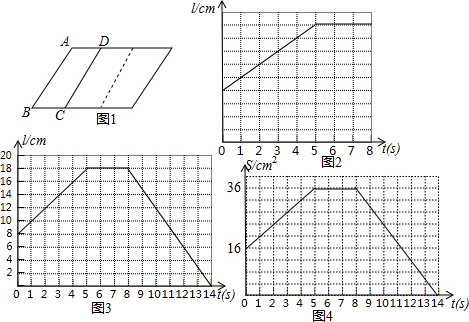
分析 （1）根据自变量、因变量的概念解答即可；
（2）根据图象确定DC边没有运动时，底边BC长度；
（3）根据图象中BC的长度变化确定DC边向右运动的时间；
（4）根据图象中BC的长度变化确定DC边在5s后的运动情况；
（5）根据图4中面积S随时间t变化的情况，找出相应的时间BC的长度，计算即可．

解答 解：（1）这个变化过程中，自变量是时间t、因变量BC的长度l；
（2）DC边没有运动时，底边BC长度是8cm；
（3）DC边向右运动了5s；
（4）由图3、图2可知，DC边在5s后停止运动3s，再向左运动6s，与AB重合；
（5）①∵DC边没有运动时，底边BC长度8cm，面积为16cm²，
∴BC边上的高为2cm²；
②由图象可知，DC边向右运动了5s后，BC=18，
∴运动的速度是2cm/s，
∴当t=2s时，面积S的值为24cm²，
由图象可知，当t=12s时，BC=6cm，
则面积S的值为12cm²，
故答案为：①2；②24；12．

点评 本题考查的是动点问题的函数图象，正确读懂图象信息、掌握函数的性质是解题的关键．