
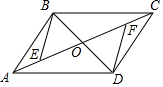
 如图,?ABCD的对角线AC、BD相交于点O,AE=CF.
如图,?ABCD的对角线AC、BD相交于点O,AE=CF.分析 (1)根据平行四边形的性质得出BO=DO,AO=OC,求出OE=OF,根据全等三角形的判定定理推出即可;
(2)根先推出四边形EBFD是平行四边形,再根据矩形的判定得出即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=OC,
∵AE=CF,
∴AO-AE=OC-CF,
即:OE=OF,
在△BOE和△DOF中,
$\left\{\begin{array}{l}OB=OD\\∠BOE=∠DOF\\ OE=OF\end{array}\right.$
∴△BOE≌△DOF(SAS);
(2)矩形,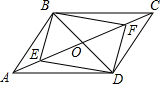
证明:∵BO=DO,OE=OF,
∴四边形BEDF是平行四边形,
∵BD=EF,
∴平行四边形BEDF是矩形.
点评 本题考查了平行四边形的性质和判定,全等三角形的判定和矩形的判定,能灵活运用定理进行推理是解此题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源:2016-2017学年山东省文慧学校八年级下学期第一次月考数学试卷(解析版) 题型:填空题
若不等式(a-1)x>a-1的解集是x<1,则a的值满足____________
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
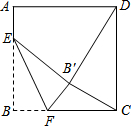 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com