
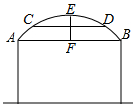
 某村想在村口建一个牌门,村长根据往来车辆的高度、宽度画了图纸如图,交给小张制作.小张看到图纸很困惑,因为他发现牌门的下部分是矩形,而上部分不知是圆弧还是抛物线形状.图纸上只标明了跨度AB为4米,最高处点E到AB的距离EF为1米,与AB平行的横梁CD到AB的距离FG为0.5米,CD为3米.请你能帮小张解决困惑,写出解题过程.
某村想在村口建一个牌门,村长根据往来车辆的高度、宽度画了图纸如图,交给小张制作.小张看到图纸很困惑,因为他发现牌门的下部分是矩形,而上部分不知是圆弧还是抛物线形状.图纸上只标明了跨度AB为4米,最高处点E到AB的距离EF为1米,与AB平行的横梁CD到AB的距离FG为0.5米,CD为3米.请你能帮小张解决困惑,写出解题过程. 分析 假设A、E、B在⊙O上,连接AO、OC、EF交CD于H.设⊙O的半径为r.利用勾股定理求出OA、CO,只要证明OA=OC即可解决问题.
解答 解:结论:图纸是上部分是圆弧.理由如下:
假设A、E、B在⊙O上,连接AO、OC、EF交CD于H.设⊙O的半径为r.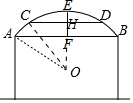
∵E是最高点,
∴$\widehat{AE}$=$\widehat{BE}$,
∴OE⊥AB,∵AB∥CD,
∴OE⊥CD,
∴AF=FB=2,CH=HD=$\frac{3}{2}$,
在Rt△AFH中,∵AO2=AF2+OF2,
∴r2=22+(r-1)2,
∴r=$\frac{5}{2}$,
在Rt△OCH中,CH=$\frac{3}{2}$,OH=$\frac{5}{2}$-$\frac{1}{2}$=2,
∴OC=$\sqrt{C{H}^{2}+O{H}^{2}}$=$\sqrt{(\frac{3}{2})^{2}+{2}^{2}}$=$\frac{5}{2}$,
∴CO=OA,
∴点C在⊙O上,
∴图纸是上部分是圆弧.
点评 本题考查圆、垂径定理、勾股定理平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考创新题目.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{3-m}$ | B. | $\sqrt{m-3}$ | C. | $\sqrt{3-m}$ | D. | $\frac{\sqrt{3-m}}{3-m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
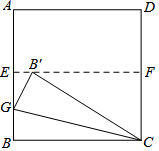 如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度.
如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.则∠B′GC=75度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3m+4=0变形为3m=-4 | B. | $\frac{x+4}{3}$=1-x变形为x+4=3-3x | ||
| C. | -5(x-2)=-5变形为x-2=1 | D. | -$\frac{x+1}{3}$=$\frac{1}{3}$变形为-x+1=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,4) | B. | (-3,-4) | C. | (3,4) | D. | (3,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com