
【题目】如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G. 
(1)求证:△CEG是等边三角形;
(2)若矩形的一边AD=3,求另一边AB的长.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC即AD∥GC,
∴∠G=∠AEF=60°,
由折叠可知:∠CED=∠CEG,而∠GED=180°﹣∠AEF=120°
∴∠GEC=∠CED= ![]() ∠GED=60°即∠G=∠GEC=60°,
∠GED=60°即∠G=∠GEC=60°,
∴△CEG是等边三角形;
(2)解:∵四边形ABCD是矩形∴∠A=∠D=90°,AB=CD,
由(1)可知∠AEF=∠CED=60°,∴∠AFE=∠DCE=30°,
∴EF=2AE,CE=2DE.设AE=x,则EF=2x,ED=EF=2x,
∴AD=x+2x=3,CE=4x,解得,x=1,DE=2,CE=4,
在Rt△CDE中,CD= ![]()
∴AB=2 ![]() .
.
【解析】(1)由折叠可知∠DEC=∠FEC,已知∠AEF=60°,可知∠DEC=∠FEC=60°,由AD∥GC,可知∠G=∠AEF=60°,故有∠G=∠FEC=60°,所以△CEG是等边三角形;(2)在Rt△AEF中,∠AEF=60°,设AE=x,则EF=2x,由折叠的性质得ED=EF=2x,根据AE+ED=AD,列方程求x,在Rt△CDE中,DE=2,∠DEC=60°,可得CE=2DE=4,利用勾股定理可求CD,即AB的长.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
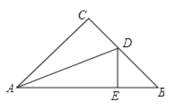
A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )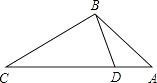
A.∠ABD=∠C
B.∠ADB=∠ABC
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.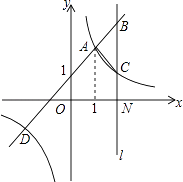
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知C是∠AOB的平分线上一点,点P,P′分别在边OA,OB上,如果要得到OP=OP′,需要添加以下条件中的某一个,那么所有可能结果的序号为________.
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
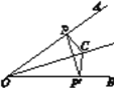
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com