
 如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.分析 (1)由EF垂直平分线段AC,可得AF=FC,EA=EC,再证明△AOF≌△COE(AAS),推出AF=CE,可得AF=CF=CE=AE,由此即可解决问题;
(2)求出EC的长,根据四边形AECF的面积=EC×AB,计算即可;
解答 (1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠AFO=∠CEO}\\{∠AOF=∠COE}\\{OA=OC}\end{array}\right.$,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=$\sqrt{6}$,
在Rt△CDF中,cos∠DCF=$\frac{CD}{CF}$,∠DCF=30°,
∴CF=$\frac{CD}{cos30°}$=2$\sqrt{2}$,
∵四边形AECF是菱形,
∴CE=CF=2$\sqrt{2}$,
∴四边形AECF的面积为:EC×AB=2$\sqrt{2}$×$\sqrt{6}$=4$\sqrt{3}$.
点评 本题考查矩形的性质、菱形的判定和性质、解直角三角形等知识,解题的关键是熟练掌握基本知识,灵活运用知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明、小华利用五一假期结伴游览某旅游景点,她们想测量景点内一条小河的宽度,如图,已知观测点C距离地面高度CH=40m,她们测得正前方河两岸A、B两点处的俯角分别为45°和30°,请计算出该处的河宽AB约为多少米?(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
小明、小华利用五一假期结伴游览某旅游景点,她们想测量景点内一条小河的宽度,如图,已知观测点C距离地面高度CH=40m,她们测得正前方河两岸A、B两点处的俯角分别为45°和30°,请计算出该处的河宽AB约为多少米?(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请根据下列图表信息解答问题:
请根据下列图表信息解答问题:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年增长率 | 31% | 27% | 32% | 35% | 52% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
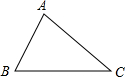 如图,已知△ABC,∠BAC=90°.
如图,已知△ABC,∠BAC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com