
【题目】如图,抛物线y=-![]() x2+
x2+![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)若该抛物线的顶点是点D,求四边形OCDB的面积;
(3)已知点P是该抛物线对称轴的一点,若以点P,O,D为顶点的三角形是等腰三角形,请直接写出点P的坐标.(不用说理)

【答案】(1)点A坐标为(-1,0),点B坐标为(3,0),点C坐标为![]() ;(2)
;(2)![]() ;(3)点P坐标为(1,0)或(1,1+
;(3)点P坐标为(1,0)或(1,1+![]() )或(1,1-
)或(1,1-![]() )或(1,-1).
)或(1,-1).
【解析】
(1)令y=0,可得方程-![]() x2+
x2+![]() x+
x+![]() =0,解方程求得x的值,即可得抛物线与x轴的交点坐标;把x=0代入函数的解析式求得y的值,即可得抛物线与y轴的交点坐标;(2)先求得顶点d的坐标,再由四边形OCDB的面积=△OCD的面积+△OBD的面积即可求得四边形OCDB的面积;(3)分OD=OP、OD=DP和OP=PD三种情况求点P的坐标即可.
=0,解方程求得x的值,即可得抛物线与x轴的交点坐标;把x=0代入函数的解析式求得y的值,即可得抛物线与y轴的交点坐标;(2)先求得顶点d的坐标,再由四边形OCDB的面积=△OCD的面积+△OBD的面积即可求得四边形OCDB的面积;(3)分OD=OP、OD=DP和OP=PD三种情况求点P的坐标即可.
(1)当y=0时,即-![]() x2+
x2+![]() x+
x+![]() =0,
=0,
解得x1=3,x2=-1,
又点A在点B的左侧,
所以点A坐标为(-1,0),点B坐标为(3,0).
当x=0时,y=![]() ,
,
点C坐标为![]() .
.
(2)y=-![]() x2+
x2+![]() x+
x+![]() =-
=-![]() (x-1)2+1,
(x-1)2+1,
所以顶点D的坐标为(1,1),
所以四边形OCDB的面积=△OCD的面积+△OBD的面积=![]() ×1+
×1+![]() ×3×1=
×3×1=![]() .
.
(3)分三种情况:
①当OD=OP时,如图1,
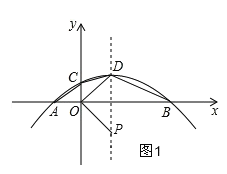
P与D关于x轴对称,
∵D(1,1),
∴P(1,-1),
②当OD=DP时,如图2,
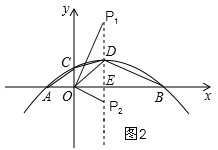
∵D(1,1),
∴OE=DE=1,
∴OD=![]() ,
,
∴PD=OD=![]() ,
,
∴P1(1,1+![]() ),P2(1,1-
),P2(1,1-![]() ),
),
③如图3,
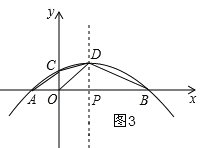
∵D(1,1),
∴当P在x轴上时,OP=PD=1,
∴P(1,0);
综上所述,点P的坐标为:(1,1)或(1,1+![]() )或(1,1-
)或(1,1-![]() )或(1,0).
)或(1,0).


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】在一次数学活动课中,某数学小组探究求环形花坛(如图所示)面积的方法,现有以下工具;①卷尺;②直棒EF;③T型尺(CD所在的直线垂直平分线段AB).
(1)在图1中,请你画出用T形尺找大圆圆心的示意图(保留画图痕迹,不写画法);
(2)如图2,小华说:“我只用一根直棒和一个卷尺就可以求出环形花坛的面积,具体做法如下:
将直棒放置到与小圆相切,用卷尺量出此时直棒与大圆两交点M,N之间的距离,就可求出环形花坛的面积”如果测得MN=10m,请你求出这个环形花坛的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-3与直线y=kx(k≠0)相交于点A和点B,则一元二次方程x2-kx-3=0的解的情况是( )

A. 有两个不相等的正实根 B. 有两个不相等的负实根
C. 一个正实根、一个负实根 D. 有两个相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一动点(不与点B,C重合),在AD右侧作△ADE,使得AD=AE,∠DAE=∠BAC,联结DE,CE。


(1)当点D在BC边上时,求证:EC=DB;
(2)当EC∥AB,若△ABD的最小角为20°,请写出ADB的度数,并对其中一个答案加以证明。
答:∠ADB的度数除了20°,还可能是 (直接写出所有答案,并对其中一个答案加以证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有( )

A.2个B.3个C.4个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB。

(1)△BPQ是 三角形;
(2)求PQ的长度;
(3)求∠APB的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com