
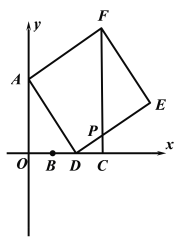
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点,以
上的动点,以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的最大值______.
的最大值______.
【答案】![]()
【解析】
作FQ⊥y轴于点Q,证△AFQ≌△DAO得FQ=OA=6,求出FQ=OC,结合FQ∥OC且∠FQO=90°证四边形OCFQ是矩形,从而得∠PCD=∠AOD=90°,设OD=x,则CD=6-x(2≤x≤6),再证△AOD∽△DCP得![]() ,即则
,即则![]() ,即PC=-
,即PC=-![]() x2+x=-
x2+x=-![]() (x-3)2+
(x-3)2+![]() ,据此可得答案.
,据此可得答案.
解:如图,作FQ⊥y轴于点Q,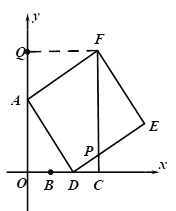
∵FQ⊥y
∴在Rt△AFQ中,∠FAQ+∠AFQ=90°,∠FQA=90°
∵四边形ADEF是正方形,
∴FA=AD,∠FAD=90°,
∴∠FAQ+∠DAO=90°,
∴∠AFQ=∠DAO,
∵∠AOD=90°
∴∠FQA=∠AOD
在△AFQ和△DAO中,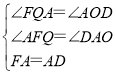
∴△AFQ≌△DAO(AAS),
∴FQ=OA=6,
∵![]()
∴FQ=OC
又∵∠FQA=∠AOD
∴FQ∥OC,
∴四边形OCFQ是平行四边形
∵∠FQO=90°,
∴四边形OCFQ是矩形,
∴∠PCD=∠AOD=90°
∴∠PDC+∠CPD=90°,
∵∠ADE=90°
∴∠ADO+∠PDC=90°,
∴∠CPD=∠ADO
∴△AOD∽△DCP,
∴![]() ,
,
设OD=x,则CD=6-x (2≤x≤6),
则![]() ,
,
即PC=-![]() x2+x=-
x2+x=-![]() (x-3)2+
(x-3)2+![]() ,
,
∴当x=3时,PC最大=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
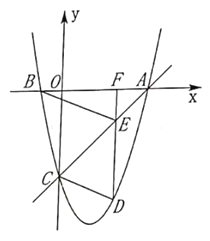
【题目】综合与探究
如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() 和点
和点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,并且与
两点,并且与![]() 轴交于另一点
轴交于另一点![]() .点
.点![]() 为第四象限抛物线上一动点(不与点
为第四象限抛物线上一动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当![]() 时,求出此时
时,求出此时![]() 的值;
的值;
(3)点![]() 在运动的过程中,
在运动的过程中,![]() 的周长是否存在最小值?若存在,求出此时
的周长是否存在最小值?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数![]() 的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
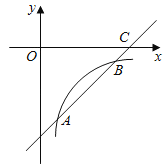
(1)求这两个函数的表达式;
(2)求△AOB的面积;
(3)请直接写出使一次函数值大于反比例函数值的x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
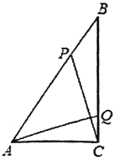
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒(
秒(![]() ),连接
),连接![]() .
.
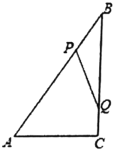
(1)若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
(2)连接![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
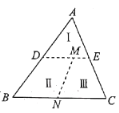
【题目】如图,现有一张三角形纸片![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点,点
中点,点![]() 是
是![]() 上一定点,点
上一定点,点![]() 是
是![]() 上一动点。将纸片依次沿
上一动点。将纸片依次沿![]() ,
,![]() 剪开,得到Ⅰ、Ⅱ和Ⅲ三部分,将Ⅱ绕点
剪开,得到Ⅰ、Ⅱ和Ⅲ三部分,将Ⅱ绕点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 重合,将Ⅲ绕点
重合,将Ⅲ绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 与
与![]() 重合,拼成了一个新的图形,则这个新图形周长的最小值是( )
重合,拼成了一个新的图形,则这个新图形周长的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 为抛物线上一点,且横纵坐标相等(原点除外),
为抛物线上一点,且横纵坐标相等(原点除外),![]() 为抛物线上一动点,过
为抛物线上一动点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,并与直线
,并与直线![]() 交于点
交于点![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)当点![]() 在线段
在线段![]() 上方时,过
上方时,过![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() ,求
,求![]() 周长的最大值及此时
周长的最大值及此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
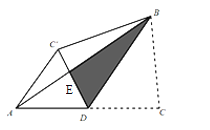
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com