
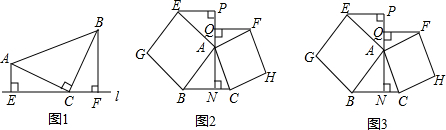
| FQ |
| AN |
| EP |
| AN |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
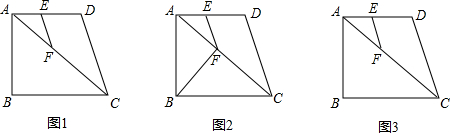
 (2011•裕华区一模)如图,已知□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,请观察下列结论:①BE=DF;②AG=GH=HC;③EG:BG=1:2;④S△AHD=2S△AGE;⑤AG;AC=1:3.其中结论正确的有(填序号)
(2011•裕华区一模)如图,已知□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,请观察下列结论:①BE=DF;②AG=GH=HC;③EG:BG=1:2;④S△AHD=2S△AGE;⑤AG;AC=1:3.其中结论正确的有(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010年中考数学模拟考试卷(浙教版)(解析版) 题型:选择题
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com