
如图,抛物线y=(x+1)2+k与x轴交于A、B两点,与y轴交于点C(0,﹣3)
(1)求抛物线的对称轴及k的值;
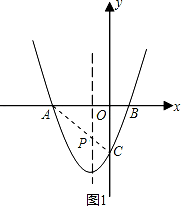
(2)抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
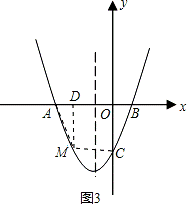
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
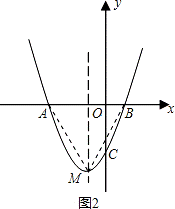
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点的坐标.
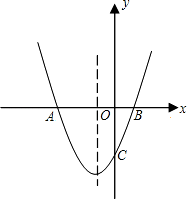
解:(1)∵抛物线y=(x+1)2+k与y轴交于点C(0,﹣3),
∴﹣3=1+k,
∴k=﹣4,
∴抛物线的解析式为:y=(x+1)2﹣4,
∴抛物线的对称轴为:直线x=﹣1;
(2)存在.
连接AC交抛物线的对称轴于点P,则PA+PC的值最小,
当y=0时,(x+1)2﹣4=0,
解得:x=﹣3或x=1,
∵A在B的左侧,
∴A(﹣3,0),B(1,0),
设直线AC的解析式为:y=kx+b,
∴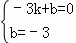 ,
,
解得: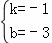 ,
,
∴直线AC的解析式为:y=﹣x﹣3,
当x=﹣1时,y=﹣(﹣1)﹣3=﹣2,
∴点P的坐标为:(﹣1,﹣2);
(3)点M是抛物线上的一动点,且在第三象限,
∴﹣3<x<0;
①设点M的坐标为:(x,(x+1)2﹣4),
∵AB=4,
∴S△AMB=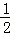 ×4×|(x+1)2﹣4|=2|(x+1)2﹣4|,
×4×|(x+1)2﹣4|=2|(x+1)2﹣4|,
∵点M在第三象限,
∴S△AMB=8﹣2(x+1)2,
∴当x=﹣1时,
即点M的坐标为(﹣1,﹣4)时,△AMB的面积最大,最大值为8;
②设点M的坐标为:(x,(x+1)2﹣4),
过点M作MD⊥AB于D,
S四边形ABCM=S△OBC+S△ADM+S梯形OCMD=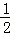 ×3×1+
×3×1+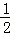 ×(3+x)×[4﹣(x+1)2]+
×(3+x)×[4﹣(x+1)2]+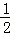 ×(﹣x)×[3+4﹣(x+1)2]
×(﹣x)×[3+4﹣(x+1)2]
=﹣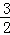 (x2+3x﹣4)=﹣
(x2+3x﹣4)=﹣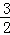 (x+
(x+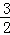 )2+
)2+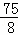 ,
,
∴当x=﹣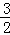 时,y=(﹣
时,y=(﹣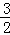 +1)2﹣4=﹣
+1)2﹣4=﹣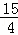 ,
,
即当点M的坐标为(﹣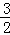 ,﹣
,﹣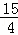 )时,四边形AMCB的面积最大,最大值为
)时,四边形AMCB的面积最大,最大值为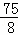 .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
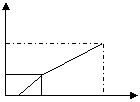
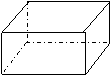
2011年3月16日上午10时福岛第一核电站第3号反应堆发生了爆炸。为了抑制核辐射进一步扩散,日本决定向6号反应堆注水冷却,铀棒被放在底面积为100m2、高为20m的长方体水槽中的一个圆柱体桶内,如图(1)所示,向桶内注入流量一定的水,注满后,继续注水,直至注满水槽为止(假设圆柱体桶在水槽中的位置始终不改变)。水槽中水面上升的高度h与注水时间t之间的函数关系如图(2)所示。
(1)求圆柱体的底面积;(2)若的圆柱体高为9m,求注水的速度及注满水槽所用时间。
 h(cm)
h(cm)
 20
20


|
查看答案和解析>>
科目:初中数学 来源: 题型:
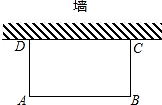
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击 成绩的平均环数
成绩的平均环数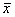 及方差
及方差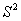 如下表所示:
如下表所示:
| 甲 | 乙 | 丙 | 丁 | |
|
|
|
|
|
|
|
| 1 | 1.1 |
|
|
若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
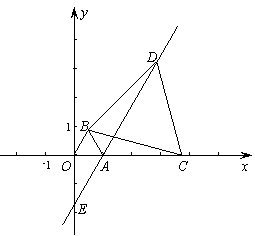
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA 为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点 ,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com