
【题目】如图,![]() 、
、![]() 、
、![]() 的平分线交于
的平分线交于![]() .
.
(1)![]() 是什么角?(直接写结果)
是什么角?(直接写结果)
(2)如图2,过点![]() 的直线交射线
的直线交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,观察线段
,观察线段![]() ,你有何发现?并说明理由.
,你有何发现?并说明理由.
(3)如图2,过点![]() 的直线交射线
的直线交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(4)如图3,过点![]() 的直线交射线
的直线交射线![]() 的反向延长线于点
的反向延长线于点![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
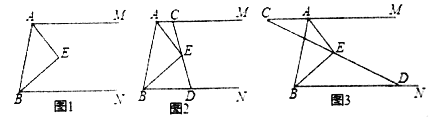
【答案】(1)直角;(2)DE=CE,理由见解析;(3)理由见解析;(4)8.
【解析】
(1)根据两直线平行同旁内角互补可得∠BAM+∠ABN=180°,然后由角平分线的定义可证∠BAE+∠ABE=90°,进而可得∠AEB=90°;
(2)过点E作EF⊥AM,交AM与F,交BN于H,作EG⊥AB于G.由角平分线的性质可证EF=EH,然后根据“AAS”证明△CEF≌△DEH即可;
(3)在AB上截取AF=AC,连接EF,可证△ACE≌△AFE,得到∠AEC=∠AEF,进而证出∠FEB=∠DEB,然后再证明△BFE≌△BDE,可得结论;
(4)延长AE交BD于F,由三线合一可知AB=BF=5,AE=EF,根据“AAS” 证明△ACE≌△FDE,可得DF=AC=3,设S△BEF=S△ABE=5x,S△DEF=S△ACE=3x,根据S△ABE﹣S△ACE=2,求出x的值,进而可求出△BDE的面积.
解:(1)∵AM//BN,
∴∠BAM+∠ABN=180°,
∵AE平分∠BAM,BE平分∠ABN,
∴∠BAE=![]() BAM,∠ABE=
BAM,∠ABE=![]() ∠ABN,
∠ABN,
∴∠BAE+∠ABE=![]() (∠BAM+∠ABN)=90°,
(∠BAM+∠ABN)=90°,
∴∠AEB=90°;
(2)如图,过点E作EF⊥AM,交AM与F,交BN于H,作EG⊥AB于G.
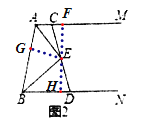
∵AE平分∠BAM,BE平分∠ABN,
∴EF=EG=EH.
∵AM//BN,
∴∠CFE=∠EHD.
在△CEF和△DEH中,
∵∠CFE=∠DHE=90°,
∠CFE=∠EHD,
EF=EH,
∴△CEF≌△DEH,
∴DE=CE;
(3)在AB上截取AF=AC,连接EF,
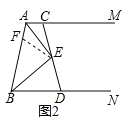
在△ACE与△AFE中,
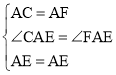 ,
,
∴△ACE≌△AFE,
∴∠AEC=∠AEF,
∵∠AEB=90°,
∴∠AEF+∠BEF=∠AEC+∠BED=90°,
∴∠FEB=∠DEB,
在△BFE与△BDE中,
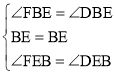 ,
,
∴△BFE≌△BDE,
∴BF=BD,
∵AB=AF+BF,
∴AC+BD=AB;
(4)延长AE交BD于F,

∵∠AEB=90°,
∴BE⊥AF,
∵BE平分∠ABN,
∴AB=BF=5,AE=EF,
∵AM//BN,
∴∠C=∠EDF,
在△ACE与△FDE中,
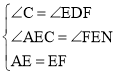 ,
,
∴△ACE≌△FDE,
∴DF=AC=3,
∵BF=5,
∴设S△BEF=S△ABE=5x,S△DEF=S△ACE=3x,
∵S△ABE﹣S△ACE=2,
∴5x﹣3x=2,
∴x=1,
∴△BDE的面积=8.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车开往距离出发地![]() 的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前
的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前![]() 到达目的地,设前一个小时的行驶速度为
到达目的地,设前一个小时的行驶速度为![]()
(1)直接用![]() 的式子表示提速后走完剩余路程的时间为
的式子表示提速后走完剩余路程的时间为
(2)求汽车实际走完全程所花的时间.
(3)若汽车按原路返回,司机准备一半路程以![]() 的速度行驶,另一半路程以
的速度行驶,另一半路程以![]() 的速度行驶(
的速度行驶(![]() ),朋友提醒他一半时间以
),朋友提醒他一半时间以![]() 的速度行驶,另一半时间以
的速度行驶,另一半时间以![]() 的速度行驶更快,你觉得谁的方案更快?请说明理由.
的速度行驶更快,你觉得谁的方案更快?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“军运会”期间,某纪念品店老板用5000元购进一批纪念品,由于深受顾客喜爱,很快售完,老板又用6000元购进同样数目的这种纪念品,但第二次每个进价比第一次每个进价多了2元.
(1)求该纪念品第一次每个进价是多少元?
(2)老板以每个15元的价格销售该纪念品,当第二次纪念品售出![]() 时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?
时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
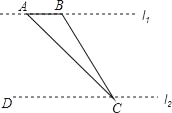
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了美化校园环境,计划购进桂花树和黄桷树两种树苗共200棵,现通过调查了解到:若购进15棵桂花树和6棵黄桷树共需600元,若购进12棵桂花树和5棵黄桷树共需490元.
(1)求购进的桂花树和黄桷树的单价各是多少元?
(2)已知甲、乙两个苗圃的两种树苗销售价格和上述价格一样,但有如下优惠:甲苗圃:每购买一棵黄桷树送两棵桂花树,购买的其它桂花树打9折.乙苗圃:购买的黄桷树和桂花树都打7折.设购买黄桷树x棵,y1和y2分别表示到甲、乙两个苗圃中购买树苗所需总费用,求出y1和y2关于x的函数表达式;
(3)现在,学校根据实际需要购买的黄桷树的棵数不少于35棵且不超过40棵,请设计一种购买方案,使购买的树苗所花费的总费用最少.最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q.
(1)求∠BPQ的度数;
(2)若PQ=3,EP=1,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张背面看上去无差别的扑克牌,正面分别写着5,6,7,8,9,洗匀后正面向下放在桌子上,从中随机抽取2张,抽出的卡片上的数字恰好是两个连续整数的概率是__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com