
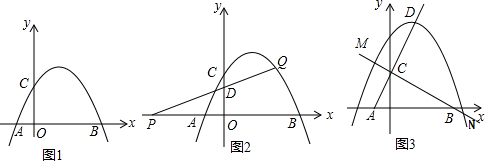
分析 (1)令y=0求出点A、B坐标,再由tan∠ACO=$\frac{1}{2}$求出点C坐标即可求出a.
(2)构造等腰直角三角形△PEF,由AC∥EF得到∠PDA=∠PEF=45°,即可解决问题.
(3)可以设M、N的横坐标分别为-t,4t,由方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=-\frac{1}{2}(x-m)^{2}+2m+2}\end{array}\right.$消去y得到:x2-(2m+1)x+m2-4m=0,再利用根与系数的关系求出m.
解答 解:(1)令y=O得ax2-3ax-4a=0,解得x1=-1,x2=4,
∴A(-1,0),B(4,0),
∵tan∠ACO=$\frac{1}{2}$,
∴$\frac{AO}{CO}=\frac{1}{2}$,
∴CO=2,
∴-4a=2,
a=-$\frac{1}{2}$,
∴抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)存在.理由如下:
在图1中,取点E(0,1),F(-2,-3),作直线PE交AC于D,交抛物线于Q,作FH⊥PO垂足为H.
在△POE和△FHP中,
$\left\{\begin{array}{l}{PO=HF}\\{∠POE=∠PHF}\\{EO=PH}\end{array}\right.$,
∴△POE≌△FHP,
∴PE=PF,∠EPO=∠PFH,
∵∠PFH+∠FPH=90°,
∴∠EPO+∠FPH=90°,
∴∠EPF=90°,∠PEF=∠PF=45°,
设直线EF的解析式为y=kx+b,E、F的坐标代入得$\left\{\begin{array}{l}{b=2}\\{-2k+b=-3}\end{array}\right.$,∴$\left\{\begin{array}{l}{k=2}\\{b=1}\end{array}\right.$,
∴直线EF为y=2x+1,
设直线AC为y=k′x+b′,A、C的坐标代入得$\left\{\begin{array}{l}{b′=2}\\{-k′+b′=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{k′=2}\\{b′=2}\end{array}\right.$,
∴直线AC为y=2x+2,
∴AC∥EF,
∴∠PDA=∠PEF=45°,
∴直线PQ满足条件,设直线PQ为y=k″x+b″,P、E坐标代入得$\left\{\begin{array}{l}{b″=1}\\{-3k″+b″=0}\end{array}\right.$∴$\left\{\begin{array}{l}{k″=\frac{1}{3}}\\{b″=1}\end{array}\right.$,
∴直线PQ为y=$\frac{1}{3}$x+1,
由$\left\{\begin{array}{l}{y=\frac{1}{3}x+1}\\{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.或\left\{\begin{array}{l}{x=-\frac{2}{3}}\\{y=\frac{7}{9}}\end{array}\right.$,
∴点Q(3,2).
(3)存在.理由如下:
∵抛物线的顶点在直线AC上,
∴可以设新抛物线为y=-$\frac{1}{2}$(x-m)2+2m+2,
∵$\frac{{S}_{△DMC}}{{S}_{△DNC}}=\frac{1}{4}$,可以设M、N的横坐标分别为-t,4t,
易知直线BC为y=-$\frac{1}{2}x$+2,
由$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=-\frac{1}{2}(x-m)^{2}+2m+2}\end{array}\right.$消去y得到:x2-(2m+1)x+m2-4m=0,
由题意$\left\{\begin{array}{l}{-t+4t=2m+1}\\{-t•4t={m}^{2}-4m}\end{array}\right.$,解得m=$\frac{2}{5}$.
∴新抛物线为y=-$\frac{1}{2}(x-\frac{2}{5})^{2}+\frac{14}{5}$.
点评 本题考查二次函数的图象问题、全等三角形的判定和性质、根与系数关系等知识,构造等腰直角三角形创造45°是解题的关键,本题综合性强,需要灵活运用方程与函数的关系解决问题.


科目:初中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=$\frac{2}{x}$ | C. | y=$\frac{x}{2}$ | D. | y=$\frac{1}{2}x+1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小刚、小明一起去精品文具店买同种钢笔和同种练习本.下面是小刚、小明与售货员的对话:
如图,小刚、小明一起去精品文具店买同种钢笔和同种练习本.下面是小刚、小明与售货员的对话:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD为BC边上的中线,若∠BAC<90°,作EA⊥AC,FA⊥BA,且AE=AC,AF=AB.连接EF,写出AD与EF的数量关系,并证明.
如图,在△ABC中,AD为BC边上的中线,若∠BAC<90°,作EA⊥AC,FA⊥BA,且AE=AC,AF=AB.连接EF,写出AD与EF的数量关系,并证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com