
【题目】已知:点A在射线CE上,∠C=∠D.
⑴如图1,若AD∥BC,求证:BD∥AC;
⑵如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
⑶如图3,在⑵的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

【答案】(1)见解析;(2)∠DAE+2∠C=90 ;(3)99°
【解析】
(1)根据AC∥BD,可得∠DAE=∠D,再根据∠C=∠D,即可得到∠DAE=∠C,进而判定AD∥BC;
(2)根据∠CGB是△ADG是外角,即可得到∠CGB=∠D+∠DAE,再根据△BCG中,∠CGB+∠C=90°,即可得到∠D+∠DAE+∠C=90°,进而得出2∠C+∠DAE=90°;
(3)设∠DAE=α,则∠DFE=8α,∠AFD=180°-8α,根据DF∥BC,即可得到∠C=∠AFD=180°-8α,再根据2∠C+∠DAE=90°,即可得到2(180°-8α)+α=90°,求得α的值,即可运用三角形内角和定理得到∠BAD的度数.
解:(1)∵AC∥BD,
∴∠DAE=∠D,
又∵∠C=∠D,
∴∠DAE=∠C,
∴AD∥BC;
(2)∠EAD+2∠C=90°.
证明:设CE与BD交点为G,
∵∠CGB是△ADG是外角,
∴∠CGB=∠D+∠DAE,
∵BD⊥BC,
∴∠CBD=90°,
∴△BCG中,∠CGB+∠C=90°,
∴∠D+∠DAE+∠C=90°,
又∵∠D=∠C,
∴2∠C+∠DAE=90°;
(3)设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=![]() ∠CBD=45°,
∠CBD=45°,
∴△ABD中,∠BAD=180°﹣45°﹣36°=99°.


科目:初中数学 来源: 题型:
【题目】已知![]() 的一条边
的一条边![]() 的长为5,另两边
的长为5,另两边![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根.
的两个实数根.
(1)求证:无论![]() 为何值,方程总有两个不相等的实数根;
为何值,方程总有两个不相等的实数根;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形,并求出
为直角三角形,并求出![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某款篮球架的示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.26,sin75°≈0.97,tan75°≈3.73, ![]() ≈1.73)( )
≈1.73)( )
A.3.04
B.3.05
C.3.06
D.4.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:![]()
⑴根据如图1,写出一个等式:
⑵如图2,若长方形的长AB为10,AD宽为6,分别求a、b的值;
⑶如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=6,ab=10,请求出阴影部分的面积.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司生产的960件新产品需要精加工后才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的![]() ,甲、乙两个工厂每天各能加工多少个新产品?
,甲、乙两个工厂每天各能加工多少个新产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE= ![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个钝角△ABC(其中∠ABC=120°)绕
点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.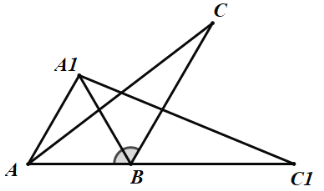
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com