
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌНтОіЫљЬсЕФЮЪЬтЃК
ЙДЙЩЖЈРэa+b=cБОЩэОЭЪЧвЛИіЙигкaЃЌbЃЌcЕФЗНГЬЃЌЮвУЧжЊЕРетИіЗНГЬгаЮоЪ§зщНтЃЌТњзуИУЗНГЬЕФе§ећЪ§НтЃЈaЃЌbЃЌcЃЉЭЈГЃНазіЙДЙЩЪ§зщЃЎЙигкЙДЙЩЪ§зщЕФбаОПЮвЙњРњЪЗЩЯгаЗЧГЃЛдЛЭЕФГЩОЭЃЌИљОнЮвЙњЙХДњЪ§бЇЪщЁЖжмїТЫуОЁЗМЧдиЃЌдкдМЙЋдЊЧА1100ФъЃЌШЫУЧОЭвбОжЊЕРЁАЙДЙуШ§ЁЂЙЩаоЫФЁЂОЖгчЮхЁБЃЈЙХШЫАбНЯЖЬЕФжБНЧБпГЦЮЊЙДЃЌНЯГЄЕФжБНЧБпГЦЮЊЙЩЃЌЖјаББпдђЮЊЯвЃЉЃЌМДжЊЕРСЫЙДЙЩЪ§зщЃЈ3ЃЌ4ЃЌ5ЃЉЃЎРрЫЦЕиЃЌЛЙПЩвдЕУЕНЯТСаЙДЙЩЪ§зщЃКЃЈ3ЃЌ4ЃЌ5ЃЉЃЌЃЈ5ЃЌ12ЃЌ13ЃЉЃЌЃЈ7ЃЌ24ЃЌ25ЃЉЃЌЃЈ9ЃЌ40ЃЌ41ЃЉЃЌЁЕШЕШЃЌетаЉЪ§зщвВНазіБЯДяИчРЫЙЙДЙЩЪ§зщЃЎ
ЩЯЪіЙДЙЩЪ§зщЕФЙцТЩЃЌПЩвдгУЯТУцБэИёжБЙлБэЪОЃК
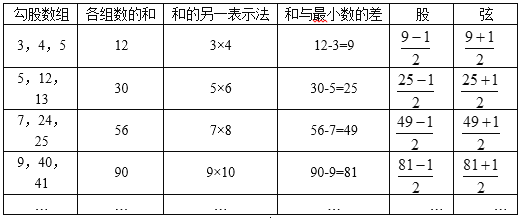
ЙлВьЗжЮіЩЯЪіЙДЙЩЪ§зщЃЌПЩвдПДГіЫќУЧОпгаШчЯТЬиЕуЃК
ЬиЕу1ЃКзюаЁЕФЙДЙЩЪ§ЕФЦНЗНЕШгкСэСНИіЙДЙЩЪ§ЕФКЭЃЛ
ЬиЕу2ЃК____________________________________ЃЎ
Ё
бЇЯАШЮЮёЃК
ЃЈ1ЃЉЧыФудйаДГіЩЯЪіЙДЙЩЪ§зщЕФвЛИіЬиЕуЃК________________ЃЛ
ЃЈ2ЃЉШчЙћnБэЪОБШ1ДѓЕФЦцЪ§ЃЌдђЩЯЪіЙДЙЩЪ§зщПЩвдБэЪОЮЊЃЈnЃЌ______ЃЌ______ЃЉ
ЃЈ3ЃЉЧыФужЄУїЃЈ2ЃЉЕФНсТлЃЎ
ЁОД№АИЁПЃЈ1ЃЉзюаЁЕФЙДЙЩЪ§гыБШЫќДѓ1ЕФећЪ§ЕФГЫЛ§ЕШгкИїИіЙДЙЩЪ§ЕФКЭЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉМћНтЮіЃЎ
ЃЛЃЈ3ЃЉМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩ3ЁС4=3+4+5ЃЌ5ЁС6=5+12+13ЃЌ7ЁС8=7+24+25ЃЌЁЁПЩЕУзюаЁЕФЙДЙЩЪ§гыБШЫќДѓ1ЕФећЪ§ЕФГЫЛ§ЕШгкИїИіЙДЙЩЪ§ЕФКЭЃЌМДПЩЕУД№АИЃЛ
ЃЈ2ЃЉгЩ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ![]() ЃЌ
ЃЌ![]() =13ЃЛ
=13ЃЛ![]() ЃЌ
ЃЌ![]() ЁЁПЩЕУЙДЪ§ЮЊДѓгк1ЕФЦцЪ§ЪБЃЌЙЩЪ§ЕШгкЙДЪ§ЕФЦНЗНМѕ1ЕФвЛАыЃЌЯвЪ§ЕШгкЙДЪ§ЕФЦНЗНМг1ЕФвЛАыЃЌМДПЩЕУД№АИЃЛ
ЁЁПЩЕУЙДЪ§ЮЊДѓгк1ЕФЦцЪ§ЪБЃЌЙЩЪ§ЕШгкЙДЪ§ЕФЦНЗНМѕ1ЕФвЛАыЃЌЯвЪ§ЕШгкЙДЪ§ЕФЦНЗНМг1ЕФвЛАыЃЌМДПЩЕУД№АИЃЛ
ЃЈ3ЃЉИљОнећЪНЕФдЫЫуЕУГіn2+(![]() )2=(
)2=(![]() )2МДПЩЃЎ
)2МДПЩЃЎ
ЃЈ1ЃЉ3ЁС4=3+4+5ЃЌ
5ЁС6=5+12+13ЃЌ
7ЁС8=7+24+25ЃЌ
ЁЁ
ЁрзюаЁЕФЙДЙЩЪ§гыБШЫќДѓ1ЕФећЪ§ЕФГЫЛ§ЕШгкИїИіЙДЙЩЪ§ЕФКЭЃЎ
ЙЪД№АИЮЊЃКзюаЁЕФЙДЙЩЪ§гыБШЫќДѓ1ЕФећЪ§ЕФГЫЛ§ЕШгкИїИіЙДЙЩЪ§ЕФКЭ
ЃЈ2ЃЉ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() =13ЃЌ
=13ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁЁ
ЁрЙЩЪ§ЕШгкЙДЪ§ЕФЦНЗНМѕ1ЕФвЛАыЃЌЯвЪ§ЕШгкЙДЪ§ЕФЦНЗНМг1ЕФвЛАыЃЌ
ЁрЙДЪ§ЮЊДѓгк1ЕФЦцЪ§ЪБЃЌЙЩЪ§ЕШгкЙДЪ§ЕФЦНЗНМѕ1ЕФвЛАыЃЌЯвЪ§ЕШгкЙДЪ§ЕФЦНЗНМг1ЕФвЛАыЃЌ
ЁрnЮЊБШ1ДѓЕФЦцЪ§ЪБЃЌЩЯЪіЙДЙЩЪ§зщПЩвдБэЪОЮЊЃЈnЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]()
ЃЈ3ЃЉЁп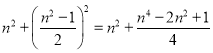
=![]()
=![]()
=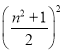 ЃЎ
ЃЎ
ЁрЃЈ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉЪЧЙДЙЩЪ§зщЃЎ
ЃЉЪЧЙДЙЩЪ§зщЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гыxжсЃЌyжсЗжБ№НЛгкЕу
гыxжсЃЌyжсЗжБ№НЛгкЕу![]() ЃЌB.Еу
ЃЌB.Еу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯвЛЕуЃЌзїжБЯп
ЩЯвЛЕуЃЌзїжБЯп![]() .
.

ЃЈ1ЃЉШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() УцЛ§ЕФШЁжЕЗЖЮЇЃЛ
УцЛ§ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШє![]() ЦНЗж
ЦНЗж![]() ЃЌМЧ
ЃЌМЧ![]() ЕФжмГЄЮЊmЃЌ
ЕФжмГЄЮЊmЃЌ![]() ЕФжмГЄЮЊnЃЌЧѓ
ЕФжмГЄЮЊnЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌAEЁЭBCНЛCBбгГЄЯпгкEЃЌCFЁЮAEНЛADбгГЄЯпгкЕуFЃЎ
(1)ЧѓжЄЃКЫФБпаЮAECFЪЧОиаЮЃЛ
(2)СЌНгOEЃЌШєcosЁЯBAEЃН![]() ЃЌABЃН5ЃЌЧѓOEЕФГЄЃЎ
ЃЌABЃН5ЃЌЧѓOEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧаЁаЧЭЌбЇЩшМЦЕФЁАЙ§жБЯпЭтвЛЕузївбжЊжБЯпЕФЦНааЯпЁБЕФГпЙцзїЭМЙ§ГЬЃК вбжЊЃКШчЭМЃЌжБЯп l КЭжБЯп l ЭтвЛЕу A
ЧѓзїЃКжБЯп APЃЌЪЙЕУ APЁЮl

зїЗЈЃКШчЭМ
ЂйдкжБЯп l ЩЯШЮШЁвЛЕу BЃЈAB гы l ВЛДЙжБЃЉЃЌвдЕу A ЮЊдВаФЃЌAB ЮЊАыОЖзїдВЃЌгыжБЯп l
НЛгкЕу CЃЎ
ЂкСЌНг ACЃЌABЃЌбгГЄ BA ЕНЕу DЃЛ
ЂлзїЁЯDACЕФЦНЗжЯпAPЃЎ
ЫљвджБЯпAPОЭЪЧЫљЧѓзїЕФжБЯпЃЌ
ИљОнаЁаЧЭЌбЇЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌЭъГЩЯТУцЕФжЄУїжЄУїЃК
ЁпABЃНACЃЌ
ЁрЁЯABCЃНЁЯACB_________ЃЈЬюЭЦРэЕФвРОнЃЉ
ЁпЁЯDAC ЪЧЁїABC ЕФЭтНЧЃЌЁрЁЯDACЃНЁЯABC+ЁЯACB
ЁрЁЯDACЃН2ЁЯABC
ЁпAP ЦНЗжЁЯDACЃЌ
ЁрЁЯDACЃН2ЁЯDAP
ЁрЁЯDAPЃНЁЯABC
ЁрAPЁЮl_________ЃЈЬюЭЦРэЕФвРОнЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЙ§жБЯпABЭтвЛЕуPзїжБЯпABЕФЦНааЯпЪБЃЌПЩвдАДШчЯТВНжшНјааЃКЂйдкжБЯпABЩЯШЮШЁСНЕуCЃЌDЃЛЂкЗжБ№вдЕуPЃЌDЮЊдВаФЃЌCDгыPCЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуEЃЛЂлзїжБЯпPEЃЌдђPEЁЮABЃЎдкЩЯУцзїЭМЙ§ГЬжаЃЌPEЁЮABЕФвРОнЪЧ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌНЋе§ЗНаЮOABCШЦЕуOФцЪБеыа§зЊ45ЁуКѓЕУЕНе§ЗНаЮOA1B1C1ЃЌвРДЫЗНЪНЃЌШЦЕуOСЌаја§зЊ2018ДЮЕУЕНе§ЗНаЮOA2018B2018C2018ЃЌШчЙћЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌФЧУДЕуB2018ЕФзјБъЮЊЃЈЁЁЁЁЃЉ
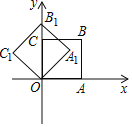
A. ЃЈ1ЃЌ1ЃЉ B. ЃЈ0ЃЌ![]() ЃЉ C. ЃЈ
ЃЉ C. ЃЈ![]() ЃЉ D. ЃЈЉ1ЃЌ1ЃЉ
ЃЉ D. ЃЈЉ1ЃЌ1ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
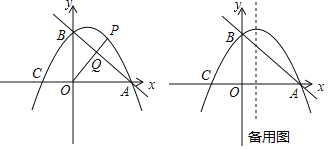
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љ![]() x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎХзЮяЯпy=Љ
x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎХзЮяЯпy=Љ![]() x2+bx+cОЙ§AЁЂBСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЎ
x2+bx+cОЙ§AЁЂBСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧЕквЛЯѓЯоХзЮяЯпЩЯЕФЕуЃЌСЌНгOPНЛжБЯпABгкЕуQЃЎЩшЕуPЕФКсзјБъЮЊmЃЌPQгыOQЕФБШжЕЮЊyЃЌЧѓyгыmЕФЙиЯЕЪНЃЌВЂЧѓГіPQгыOQЕФБШжЕЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуDЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЖЏЕуЃЌСЌНгODЁЂCDЃЌЩшЁїODCЭтНгдВЕФдВаФЮЊMЃЌЕБsinЁЯODCЕФжЕзюДѓЪБЃЌЧѓЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋХзЮяЯпMЃКy=- ![]() x2+2ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛЃЌЕУЕНХзЮяЯпM'ЃЎШєХзЮяЯпM'гыxжсНЛгкAЁЂBСНЕуЃЌM'ЕФЖЅЕуМЧЮЊCЃЌдђЁЯACB=ЃЈ ЃЉ
x2+2ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛЃЌЕУЕНХзЮяЯпM'ЃЎШєХзЮяЯпM'гыxжсНЛгкAЁЂBСНЕуЃЌM'ЕФЖЅЕуМЧЮЊCЃЌдђЁЯACB=ЃЈ ЃЉ
A.45ЁуB.60ЁуC.90ЁуD.120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвЮЊСЫЪЕЯж2020ФъШЋУцЭбЦЖФПБъЃЌЪЕЪЉЁАОЋзМЗіЦЖЁБеНТдЃЌВЩШЁвьЕиАсЧЈЃЌВњвЕЗіГжЕШДыЪЉЃЎЪЙЦЖРЇЛЇЕФЩњЛюЬѕМўЕУЕНИФЩЦЃЌЩњЛюжЪСПУїЯдЬсИпЃЎФГЦьЯиЮЊСЫШЋУцСЫНтЦЖРЇЯиЖдЗіЦЖЙЄзїЕФТњвтЖШЧщПіЃЌНјааЫцЛњГщбљЕїВщЃЌЗжЮЊЫФИіРрБ№ЃКAЃЎЗЧГЃТњвтЃЛBЃЎТњвтЃЛCЃЎЛљБОТњвтЃЛDЃЎВЛТњвтЃЎвРОнЕїВщЪ§ОнЛцжЦГЩЭМ1КЭЭМ2ЕФЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
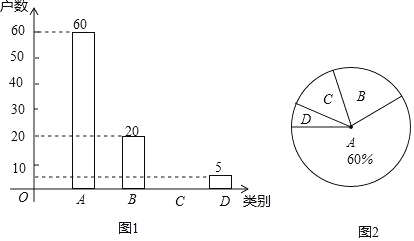
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉНЋЭМ1ВЙГфЭъећЃЛ
ЃЈ2ЃЉЭЈЙ§ЗжЮіЃЌЦЖРЇЛЇЖдЗіЦЖЙЄзїЕФТњвтЖШЃЈAЁЂBЁЂCРрЪгЮЊТњвтЃЉЪЧЁЁЁЁЃЛ
ЃЈ3ЃЉЪаЗіЦЖАьДгИУЦьЯиМзЯчеђ3ЛЇЁЂввЯчеђ2ЛЇЙВ5ЛЇЦЖРЇЛЇжаЃЌЫцЛњГщШЁСНЛЇНјааТњвтЖШЛиЗУЃЌЧѓетСНЛЇЦЖРЇЛЇЧЁКУЖМЪЧЭЌвЛЯчеђЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com