
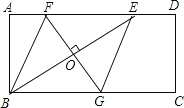
【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=![]() AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当![]() 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)
【答案】(1)菱形,理由见解析;(2)![]() ;(3)6.
;(3)6.
【解析】试题分析:(1)根据矩形和线段垂直平分线的性质,由AAS证明ΔBOF≌ΔBOG,得到BG=GE=EF=FB,从而得出四边形BFEG是菱形的结论.
(2)根据矩形和菱形的性质,反复应用勾股定理即可求得FG的长.
(3)同(2)的思路,应用特殊元素法,列出关于n的方程求解即可.
试题解析:(1)(1)菱形,理由如下:
∵FG为BE的垂直平分线,∴FE=FB,GB=GE,∠FEB=∠FBO.
又∵FE∥BG,∴∠FEB=∠GBO. ∴∠FBO=∠GBO,BO=BO,∠BOF=∠BOG.
∴ΔBOF≌ΔBOG(AAS). ∴BF=BG.
∴BG=GE=EF=FB. ∴BFEG为菱形.
(2)∵AB=a,AD=2AB, ![]() ,∴AD=2a,
,∴AD=2a, ![]() .
.
∴根据勾股定理,得 BE=![]() . ∴OE=
. ∴OE=![]() .
.
设菱形BFEG的边长为x,
∵AB2+AF2=BF2,
∴![]() ,解得:x=
,解得:x=![]() .
.
∴OF=![]() .
.
∴FG=![]() .
.
(3)n=6.


科目:初中数学 来源: 题型:
【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列问题中,两个变量成正比例的是( )
A.等腰三角形的面积一定,它的底边和底边上的高
B.等边三角形的面积和它的边长
C.长方形的一边长确定,它的周长与另一边长
D.长方形的一边长确定,它的面积与另一边长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. 2aa = 2 B. 2a + b = 2ab C. 3x2 + 2x2 = 5x4 D. mn 2mn = mn
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com