
”¾ĢāÄæ”æŅŃÖŖµćP£Øx0£¬y0£©ŗĶÖ±Ļßy£½kx+b£¬ŌņµćPµ½Ö±Ļßy£½kx+bµÄ¾ąĄėdæÉÓĆ¹«Ź½d£½![]() ¼ĘĖć£®
¼ĘĖć£®
ĄżČē£ŗĒóµćP£Ø©2£¬1£©µ½Ö±Ļßy£½x+1µÄ¾ąĄė£®
½ā£ŗŅņĪŖÖ±Ļßy£½x+1æɱäŠĪĪŖx©y+1£½0£¬ĘäÖŠk£½1£¬b£½1£®
ĖłŅŌµćP£Ø©2£¬1£©µ½Ö±Ļßy£½x+1µÄ¾ąĄėĪŖd£½![]() £½
£½![]() £½
£½![]() £½
£½![]() £®
£®
øł¾ŻŅŌÉĻ²ÄĮĻ£¬Ēó£ŗ
£Ø1£©µćP£Ø2£¬4£©µ½Ö±Ļßy£½3x©2µÄ¾ąĄė£¬²¢ĖµĆ÷µćPÓėÖ±ĻßµÄĪ»ÖĆ¹ŲĻµ£»
£Ø2£©µćP£Ø2£¬1£©µ½Ö±Ļßy£½2x©1µÄ¾ąĄė£»
£Ø3£©ŅŃÖŖÖ±Ļßy£½©3x+1Óėy£½©3x+3Ę½ŠŠ£¬ĒóÕāĮ½ĢõÖ±ĻߵľąĄė£®
”¾“š°ø”æ(1)¼ū½āĪö£»(2)![]() ;(3)
;(3)![]() .
.
”¾½āĪö”æ
£Ø1£©øł¾ŻŅŃÖŖµÄ¾ąĄė¹«Ź½¼“æÉĒóµćµ½Ö±ĻߵľąĄė£¬“Ó¶ųĖµĆ÷µćPÓėÖ±ĻßµÄĪ»ÖĆ¹ŲĻµ£»
£Ø2£©øł¾ŻŅŃÖŖµÄ¾ąĄė¹«Ź½¼“æÉĒó½ā£»
£Ø3£©ŌŚŅŃÖŖµÄŅ»ĢõÖ±ĻßÉĻČ”Ņ»µć£¬ŌŁøł¾Żµćµ½Ö±ĻߵľąĄė¹«Ź½¼“æÉĒóµĆ½įĀŪ£®
£Ø1£©”ßµćP£Ø2£¬4£©£¬
”ąµćPµ½Ö±Ļßy£½3x©2µÄ¾ąĄėĪŖ£ŗd£½![]() £½0£®
£½0£®
”ąµćPŌŚÖ±Ļßy£½3x©2ÉĻ£®
“š£ŗµćPµ½Ö±Ļßy£½3x©2µÄ¾ąĄėĪŖ0£¬µćPŌŚÖ±Ļßy£½3x©2ÉĻ£®
£Ø2£©”ßµćP£Ø2£¬©1£©
”ąµćPµ½Ö±Ļßy£½2x©1µÄ¾ąĄėĪŖ£ŗd£½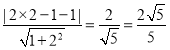 £®
£®
“š£ŗµćPµ½Ö±Ļßy£½2x©1µÄ¾ąĄėĪŖ![]() £®
£®
£Ø3£©ŌŚÖ±Ļßy£½©3x+1ČĪŅāČ”Ņ»µćP£¬µ±x£½0Ź±£¬y£½1£®
”ąP£Ø0£¬1£©£®
”ąµćPµ½Ö±Ļßy£½©3x+3µÄ¾ąĄėĪŖ£ŗd£½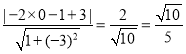 £®
£®
“š£ŗĮ½Ę½ŠŠĻßÖ®¼äµÄ¾ąĄėĪŖ![]() £®
£®


 Źī¼Ł×÷ŅµŹī¼ŁæģĄÖĮ·Ī÷°²³ö°ęÉēĻµĮŠ“š°ø
Źī¼Ł×÷ŅµŹī¼ŁæģĄÖĮ·Ī÷°²³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćP£Ø1£¬2£©£¬”ŃP¾¹żŌµćO£¬½»yÖįÕż°ėÖįÓŚµćA£¬µćBŌŚ”ŃPÉĻ£¬”ĻBAO£½45”ć£¬ŌņµćBµÄ×ų±źŹĒ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŅŌµćOĪŖŌ²ŠÄµÄĮ½øöĶ¬ŠÄŌ²ÖŠ£¬“óŌ²µÄĻŅAB½»Š”Ō²ÓŚµćC”¢D£®
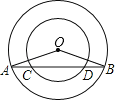
£Ø1£©ĒóÖ¤AC£½BD£»
£Ø2£©ČōAC£½3£¬“óŌ²ŗĶŠ”Ō²µÄ°ė¾¶·Ö±šĪŖ6ŗĶ4£¬ŌņCDµÄ³¤¶ČŹĒ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
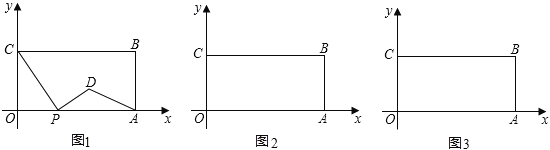
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¾ŲŠĪOABCµÄĮ½±ßOA”¢OC·Ö±šŌŚxÖį”¢yÖįµÄÕż°ėÖįÉĻ£¬OA=4£¬OC=2£®µćP“ÓµćO³ö·¢£¬ŃŲxÖįŅŌĆæĆė1øöµ„Ī»³¤µÄĖŁ¶ČĻņµćAŌČĖŁŌĖ¶Æ£¬µ±µćPµ½“ļµćAŹ±Ķ£Ö¹ŌĖ¶Æ£¬ÉčµćPŌĖ¶ÆµÄŹ±¼äŹĒtĆė£®½«Ļ߶ĪCPµÄÖŠµćČʵćP°“Ė³Ź±Õė·½ĻņŠż×Ŗ90”ćµĆµćD£¬µćDĖęµćPµÄŌĖ¶Æ¶ųŌĖ¶Æ£¬Į¬½ÓDP”¢DA£®
£Ø1£©µ±t=2Ź±£¬µćDµÄ×ų±źŹĒ £»
£Ø2£©ĒėÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾³öµćDµÄ×ų±ź £»
£Ø3£©ŌŚµćP“ÓOĻņAŌĖ¶ÆµÄ¹ż³ĢÖŠ£¬”÷DPAÄÜ·ń³ÉĪŖÖ±½ĒČż½ĒŠĪ£æČōÄÜ£¬ĒótµÄÖµ£®Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻACB=72”ć£¬½«”÷ABCČʵćB°“ÄꏱÕė·½ĻņŠż×ŖµĆµ½”÷BDE£ØµćDÓėµć AŹĒ¶ŌÓ¦µć£¬µćEÓėµćCŹĒ¶ŌÓ¦µć£©£¬ĒŅ±ßDEĒ”ŗĆ¾¹żµćC£¬Ōņ”ĻABDµÄ¶ČŹżĪŖ
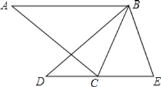
A. 36”ć B. 40”ć C. 45”ć D. 50”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
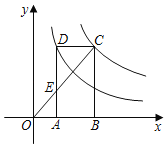
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDµÄ¶„µćC£¬D·Ö±šŌŚ·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©£®y£½
£Øx£¾0£©£®y£½![]() £Øx£¾0£©µÄĶ¼ĻóÉĻ£¬¶„µćA£¬BŌŚxÖįÉĻ£¬Į¬½ÓOC£¬½»DAÓŚµćE£¬Ōņ
£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬¶„µćA£¬BŌŚxÖįÉĻ£¬Į¬½ÓOC£¬½»DAÓŚµćE£¬Ōņ![]() £½_____£®
£½_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”ĻśŹŪŅ»ÅśĆūÅĘ³ÄÉĄ£¬Ę½¾łĆæĢģæÉŹŪ³ö20¼ž£¬Ć漞ÓÆĄū45ŌŖ£¬ĪŖĮĖĄ©“óĻśŹŪ”¢Ōö¼ÓÓÆĄū¾”æģ¼õÉŁæā“ę£¬ÉĢ³”¾ö¶Ø²ÉČ”ŹŹµ±µÄ½µ¼Ū“ėŹ©£¬¾µ÷²é·¢ĻÖ£¬Čē¹ūĆ漞³ÄÉĄĆæ½µ¼Ū1ŌŖ£¬ÉĢ³”Ę½¾łĆæĢģæɶąŹŪ³ö4¼ž£¬ČōÉĢ³”Ę½¾łĆæĢģÓÆĄū2100ŌŖ£¬Ć漞³ÄÉĄÓ¦½µ¼Ū¶ąÉŁŌŖ£æĒėĶź³ÉĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ī“½µ¼ŪÖ®Ē°£¬Ä³ÉĢ³”³ÄÉĄµÄ×ÜÓÆĄūĪŖ”” ”” ŌŖ£®
£Ø2£©½µ¼Ūŗó£¬ÉčijÉĢ³”Ć漞³ÄÉĄÓ¦½µ¼ŪxŌŖ£¬ŌņĆ漞³ÄÉĄÓÆĄū”” ””ŌŖ£¬Ę½¾łĆæĢģæÉŹŪ³ö”” ””¼ž£ØÓĆŗ¬xµÄ“śŹżŹ½½ųŠŠ±ķŹ¾£©
£Ø3£©ĒėĮŠ³ö·½³Ģ£¬Ēó³öxµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() µÄ
µÄ![]() Óė
Óė![]() µÄ²æ·Ö¶ŌÓ¦ÖµČē±ķ£ŗ
µÄ²æ·Ö¶ŌÓ¦ÖµČē±ķ£ŗ
|
| 0 | 2 | 3 | 4 |
| 5 | 0 |
|
| 0 |
ĻĀĮŠ½įĀŪ£ŗ¢ŁÅ×ĪļĻßµÄæŖæŚĻņÉĻ£»¢ŚÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļß![]() £»¢Ūµ±
£»¢Ūµ±![]() Ź±£¬
Ź±£¬![]() £»¢Ü3ŹĒ·½³Ģ
£»¢Ü3ŹĒ·½³Ģ![]() µÄŅ»øöøł£»¢ŻČō
µÄŅ»øöøł£»¢ŻČō![]() £¬
£¬![]() ŹĒÅ×ĪļĻßÉĻĮ½µć£¬Ōņ
ŹĒÅ×ĪļĻßÉĻĮ½µć£¬Ōņ![]() £¬ĘäÖŠÕżČ·µÄøöŹżŹĒ£Ø £©
£¬ĘäÖŠÕżČ·µÄøöŹżŹĒ£Ø £©
A.1B.2C.3D.4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½«ÕżĆę·Ö±šŠ“×ÅŹż×Ö1£¬2£¬3µÄČżÕÅæØʬ£Ø×¢£ŗÕāČżÕÅæØʬµÄŠĪד”¢“óŠ””¢ÖŹµŲ£¬ŃÕÉ«µČĘäĖū·½ĆęĶźČ«ĻąĶ¬£¬Čō±³ĆęÉĻ·ÅŌŚ×ĄĆęÉĻ£¬ÕāČżÕÅæØʬæ“ÉĻČ„ĪŽČĪŗĪ²ī±š£©Ļ“ŌČŗ󣬱³ĆęĻņÉĻ·ÅŌŚ×ĄĆęÉĻ£¬“ÓÖŠĻČĖ껜³éČ”Ņ»ÕÅæØʬ£¬¼ĒøĆæØʬÉĻµÄŹż×ÖĪŖx£¬ŌŁ°ŃŹ£ĻĀµÄĮ½ÕÅæØʬĻ“ŌČŗ󣬱³ĆęĻņÉĻ·ÅŌŚ×ĄĆęÉĻ£¬ŌŁ“ÓÕāĮ½ÕÅæØʬ֊Ė껜³éČ”Ņ»ÕÅæØʬ£¬¼ĒøĆæØʬÉĻµÄŹż×ÖĪŖy£®
£Ø1£©ÓĆĮŠ±ķ·Ø»ņŹ÷דĶ¼·Ø£ØŹ÷דĶ¼Ņ²³ĘŹ÷ŠĪĶ¼£©ÖŠµÄŅ»ÖÖ·½·Ø£¬Š“³ö£Øx£¬y£©ĖłÓŠæÉÄܳöĻֵĽį¹ū£®
£Ø2£©ĒóČ”³öµÄĮ½ÕÅæØʬÉĻµÄŹż×ÖÖ®ŗĶĪŖżŹżµÄøÅĀŹP£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com