
分析 (1)先算乘法,再合并同类项,最后代入求出即可;
(2)解方程组求出p、q的值,算乘方,再代入,最后求出即可.
解答 解:(1)(x-2y)2-(x-y)(x+y)-2y2
=x2-4xy+4y2-x2+y2-2y2
=-4xy+3y2
=-y(4x-3y),
∵4x=3y,
∴原式=0;
(2)$\left\{\begin{array}{l}{2p+q=\frac{17}{3}①}\\{p=-9q②}\end{array}\right.$
把②式代入①中,得-18q+q=$\frac{17}{3}$,
解之得q=-$\frac{1}{3}$
把q=-$\frac{1}{3}$代入②中,得p=3,
所以$\left\{\begin{array}{l}{p=3}\\{q=-\frac{1}{3}}\end{array}\right.$,
当p=3,q=-$\frac{1}{3}$时,
(-2p2q)0-(3pq)-2+p2014q2016
=1-(-3×3×$\frac{1}{3}$)-2+32014×(-$\frac{1}{3}$)2016
=1-$\frac{1}{9}$+[32014×(-$\frac{1}{3}$)2014]×(-$\frac{1}{3}$)2
=1-$\frac{1}{9}$+$\frac{1}{9}$
=1.
点评 本题考查了整式的混合运算和求值,解二元一次方程组,零指数幂,负整数指数幂等知识点,能正确运用知识点进行计算和化简是解此题的关键.


科目:初中数学 来源: 题型:选择题
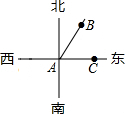 已知A、B两地的位置如图所示,且∠BAC=60°,那么下列语句正确的是( )
已知A、B两地的位置如图所示,且∠BAC=60°,那么下列语句正确的是( )| A. | A地在B地的北偏东60°方向 | B. | A地在B地的北偏东30°方向 | ||
| C. | B地在A地的北偏东60°方向 | D. | B地在A地的北偏东30°方向 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
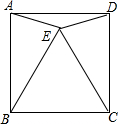 如图,在正方形ABCD中,△BCE是等边三角形,连接AE,DE.
如图,在正方形ABCD中,△BCE是等边三角形,连接AE,DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com