
| A校 | B校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | 20 | 0.15 | 10 | 0.15 |
| 乙地 | 15 | 0.20 | 20 | 0.20 |

| A校 | B校 | |
| 甲地 | 1500 | 2000 |
| 乙地 | 2100 | 400 |
| A校 | B校 | |
| 甲地 | 1100 | 2400 |
| 乙地 | 2500 | 0 |
| 分数段 | 0~4 | 5~8 | 9~12 | 13~16 | 17~20 |
| 等级 | E | D | C | B | A |


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源:不详 题型:解答题
| 5 |
| 2 |


| OG2 |
| OF |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 | 甲 | 乙 | 总计 |
| A | x | 14 | |
| B | 14 | ||
| 总计 | 15 | 13 | 28 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 3 |
| 3 |
| 3 |
 是否改变?若不变,请指出来;若改变,请写出面积变化的范围.(不必说明理由)
是否改变?若不变,请指出来;若改变,请写出面积变化的范围.(不必说明理由)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
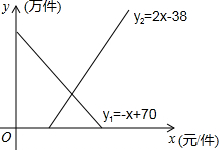
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| a2+b2 |
| A.30cm2/s | B.32cm2/s | C.34cm2/s | D.40cm2/s |
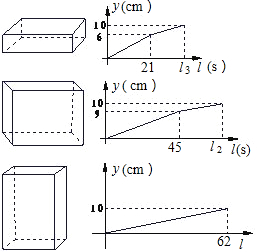
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com