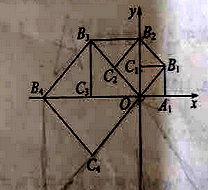
【题目】(2016山东省聊城市第17题)如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 ．
【答案】（21008，0）
【解析】
试题分析：首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标，找出这些坐标的之间的规律，然后根据规律计算出点B2016的坐标．∵正方形OA1B1C1边长为1，∴OB1=
，
∵正方形OB1B2C2是正方形OA1B1C1的对角线OB1为边，∴OB2=2，∴B2点坐标为（0，2），同理可知OB3=2，
∴B3点坐标为（﹣2，2），同理可知OB4=4，B4点坐标为（﹣4，0），
B5点坐标为（﹣4，﹣4），B6点坐标为（0，﹣8），B7（8，﹣8），B8（16，0）
B9（16，16），B10（0，32），
由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的倍，∵2016÷8=252∴B2016的纵横坐标符号与点B8的相同，横坐标为正值，纵坐标是0，
∴B2016的坐标为（21008，0）．
优加精卷系列答案科目：初中数学 来源： 题型：
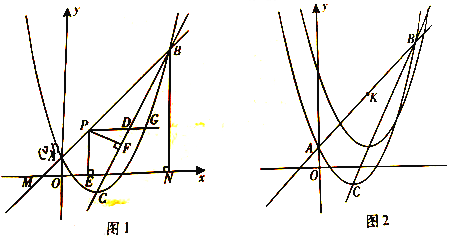
【题目】(2016重庆市第26题)如图1，二次函数
的图象与一次函数y=kx+b(k≠0)的图象交于A，B两点，点A的坐标为（0,1），点B在第一象限内，点C是二次函数图象的顶点，点M是一次函数y=kx+b(k≠0)的图象与x轴的交点，过点B作x轴的垂线，垂足为N，且S△AMO：S四边形AONB=1：48.
（1）求直线AB和直线BC的解析式；
（2）点P是线段AB上一点，点D是线段BC上一点，PD//x轴，射线PD与抛物线交于点G，过点P作PE⊥x轴于点E，PF⊥BC于点F，当PF与PE的乘积最大时，在线段AB上找一点H（不与点A，点B重合），使GH+
BH的值最小，求点H的坐标和GH+BH的最小值；
（3）如图2，直线AB上有一点K（3,4），将二次函数沿直线BC平移，平移的距离是t(t≥0)，平移后抛物线使点A，点C的对应点分别为点A’，点C’；当△A’C’K是直角三角形时，求t的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】使用计算器计算各式：6×7= ，66×67= ，666×667= ，6 666×6 667= ．
（1）根据以上结果，你发现了什么规律？
（2）依照你发现的规律，不用计算器，你能直接写出666 666×666 667的结果吗？请你试一试．
查看答案和解析>>
科目：初中数学 来源： 题型：
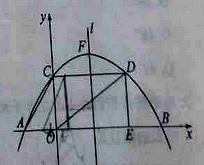
【题目】(2016山东省聊城市第25题)如图，已知抛物线y=ax2+bx+c经过点A（﹣3，0），B（9，0）和C（0，4）．CD垂直于y轴，交抛物线于点D，DE垂直与x轴，垂足为E，l是抛物线的对称轴，点F是抛物线的顶点．
（1）求出二次函数的表达式以及点D的坐标；
（2）若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合，再沿对称轴l向上平移到点C与点F重合，得到Rt△A1O1F，求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积；
（3）若Rt△AOC沿x轴向右平移t个单位长度（0＜t≤6）得到Rt△A2O2C2，Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S，求S与t之间的函数表达式，并写出自变量t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】化简下列各式，并解答问题：
①-（-2）；
②+（-
）；
③-[-（-4）]；
④-[-（+3.5）]；
⑤-{-[-（-5）]}；
⑥-{-[-（+5）]}.
问：（1）当+5前面有2 018个负号时，化简后结果是多少？
（2）当-5前面有2 019个负号时，化简后的结果是多少？你能总结出什么规律？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
