
 如图,四边形ABCD是平行四边形.
如图,四边形ABCD是平行四边形.分析 (1)由角平分线的作法,即可得出结果;
(2)由(1)得:∠ABE=∠CBE,再由平行四边形的性质得出∠ABE=∠AEB,即可得出结论.
解答 (1)解:①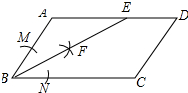 以B为圆心,适当长为半径画弧,交AB于M,BC于N,
以B为圆心,适当长为半径画弧,交AB于M,BC于N,
②分别以M、N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧交于F,
③作射线BF,交AD于E,如图所示:
(2)证明:由(1)得:∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE.
点评 本题考查了平行四边形的性质、角平分线的作图、等腰三角形的判定;熟练掌握平行四边形的性质是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )
如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )| A. | 边边边 | B. | 角边角 | C. | 边角边 | D. | 角角边 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
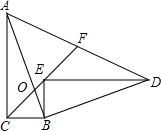 如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.
如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 看图填空:
看图填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 交通方式 | 频数(人数) | 频率 |
| 公共汽车 | m | 0.25 |
| 小车 | 24 | 0.20 |
| 摩托车 | 36 | n |
| 自行车 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com