
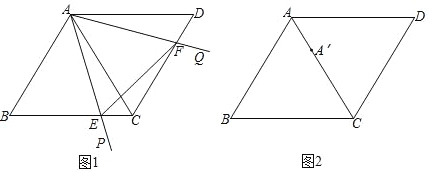
【题目】如图1,AC是边长为6的菱形ABCD的对角线,∠ABC=∠PAQ=60°,∠PAQ绕点A旋转,射线AP、AQ分别交边BC、CD于点E、F,连接EF.请探究:
(1)在旋转过程中,线段AE、AF有怎样的数量关系?并说明理由;
(2)在旋转过程中,△AEF的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由
(3)如图2,将∠PAQ沿着AC向下平移至点A处,使CA′:AA′=2:1,在∠PA′Q绕点A′旋转过程中,始终保持∠ABC=∠PA′Q,射线A′P、A′Q分别交直线BC、CD于点E、F,连接EF.当S△A′EF:S菱形ABCD=19:18时,直接写出线段CE的长.
【答案】(1)AE=AF;(2)存在,S△AEF的最小值为![]() ;(3)满足条件的EC的值为6或10.
;(3)满足条件的EC的值为6或10.
【解析】
(1)结论:AE=AF.只要证明△ACE≌△ADF即可解决问题.
(2)证明△AEF为等边三角形,故只有边长最小时,△AEF的面积才最小,当AP⊥BC时,AE为最小.
(3)分两种情形分别求解即可解决问题:①如图2中,当等E在CB的延长线上时.②如图3中,当点E在BC的延长线上时.
解:(1)结论:AE=AF.
理由:如图1中,
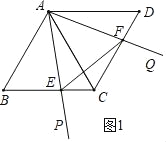
∵四边形ABCD是菱形,
∴AB=BC=CD=AD
∵∠ABC=60°,
∴∠ACE=∠ADF=60°,
∴AC=AD,
又∵∠PAQ=60°,
∴∠ACE=∠ADF=∠CAD=60°,AC=AD,
∴∠CAE=∠DAF,
∴△ACE≌△ADF(ASA),
∴AE=AF.
(2)存在.
理由:如图1中,由(1)得AE=AF,∠PAQ=60°
∴△AEF为等边三角形,
故只有边长最小时,△AEF的面积才最小,
∴当AP⊥BC时,AE为最小,
∵AB=6,
此时AE=3![]() ,则S△AEF的最小值为
,则S△AEF的最小值为![]() .
.
(3)①如图2中,当等E在CB的延长线上时,作A′H⊥BC于H.
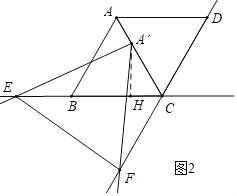
由题意菱形ABCD的面积=2×![]() ×62=18
×62=18![]() ,
,
∵S△A′EF:S菱形ABCD=19:18,
∴S△AEF=19![]() ,
,
∵△A′EF是等边三角形,
∴![]() ×A′E2=19
×A′E2=19![]() ,
,
∴A′E2=76,
在Rt△A′CH中,∵CA′=4,∠A′CH=60°,
∴CH=![]() ×4=2,A′H=2
×4=2,A′H=2![]() ,
,
∴EH=![]() =8,
=8,
∴CE=EH+CH=8+2=10.
②如图3中,当点E在BC的延长线上时,作A′H⊥BC于H.
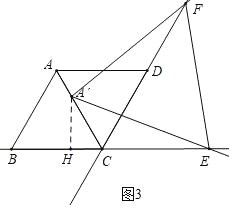
同法可证EH=8,可得EC=EH=CH=8﹣2=6,
综上所述,满足条件的EC的值为6或10.


科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数![]() (k≠0)的图象恰好经过点C和点D,则k的值为( )
(k≠0)的图象恰好经过点C和点D,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
查看答案和解析>>
科目:初中数学 来源: 题型:
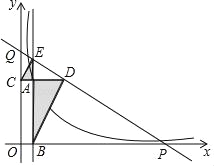
【题目】如图,已知动点A在反比例函数y=![]() (x>0)的图象上,直线PQ与x轴,y轴交于P、Q两点,过点A作CD∥x轴,交y轴于点C,交直线PQ于点D,过点A作EB∥y轴交x轴于点B,交直线PQ于点E,若CE∥BD且CA:AE=1:2,QE:DP=1:9,则阴影部分的面积为______.
(x>0)的图象上,直线PQ与x轴,y轴交于P、Q两点,过点A作CD∥x轴,交y轴于点C,交直线PQ于点D,过点A作EB∥y轴交x轴于点B,交直线PQ于点E,若CE∥BD且CA:AE=1:2,QE:DP=1:9,则阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
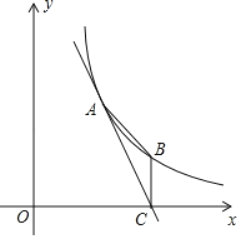
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(1)求反比例函数和直线AC的解析式;
(2)求△ABC的面积;
(3)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,请直接写出符合条件的所有D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
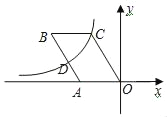
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com