
分析 (1)设这个一次函数的表达式为y=kx+b,因为两直线平行k相等易得k=2,把(-1,2)代入y=kx+b,即可求得b的值;
(2)分三种情况讨论:当点P在第一象限、第三象限、第四象限时,根据△POA的面积为3,分别代入面积公式进行计算可求得P的坐标.
解答 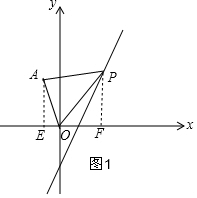 解:(1)设这个一次函数的表达式为y=kx+b,
解:(1)设这个一次函数的表达式为y=kx+b,
∵直线y=kx+b与y=2x-2平行,
∴k=2,
∵直线y=kx+b过A(-1,2),
∴2×(-1)+b=2,
解得:b=4,
∴直线解析式为y=2x+4;
(2)设P(m,2m-2),
分三种情况:
①如图1,当点P在第一象限时,过A作AE⊥x轴于E,过P作PF⊥x轴于F,
∴S△AOP=S梯形AEFP-S△AOE-S△POF=3,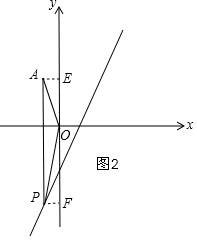
$\frac{1}{2}$(2+2m-2)(1+m)-$\frac{1}{2}$×1×2-$\frac{1}{2}$×m×(2m-2)=3,
m=2,
当m=2时,2m-2=2×2-2=2,
∴P(2,2)
②如图2,当点P在第三象限时,过A作AE⊥y轴于E,过P作PF⊥y轴于F,
∴S△AOP=S梯形AEFP-S△AOE-S△POF=3,
$\frac{1}{2}$(2-2m+2)(1-m)-$\frac{1}{2}$×1×2-$\frac{1}{2}$×(-m)×(-2m+2)=3,
m=-1,
当m=-1时,2m-2=-4,
∴P(-1,-4);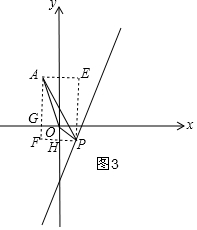
③如图3,当点P在第四象限时,构建矩形AFPE,交x轴于G,交y轴于H,
S△AOP=S△AFP-S△AOG-S矩形GFHO-S△OPH=3
$\frac{1}{2}$×(1+m)(2+2-2m)-$\frac{1}{2}$×1×2-1×(2-2m)-$\frac{1}{2}$×m×(2-2m)=3
m=2
当m=2时,2m-2=2×2-2=2,不符合题意,
综上所述,点P的坐标为(2,2)或(-1,-4).
点评 本题考查了两条直线相交和平行问题,以及一次函数图象上点的坐标特征,用到的知识点为:两直线平行,那么解析式中的比例系数相同;点在直线上的,点的横纵坐标适合这个函数解析式,即利用解析式表示该图象上谋点的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
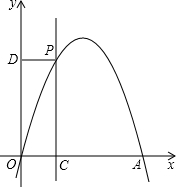 如图,在平面直角坐标系中,二次函数y=-x2+bx的图象与x轴交于点A(4,0).点P是y轴右侧抛物线上一动点(不与点A重合),过点P作直线PC⊥x轴于点C,PD⊥y轴与点D,设矩形PCOD的周长为l,点P的横坐标为m.
如图,在平面直角坐标系中,二次函数y=-x2+bx的图象与x轴交于点A(4,0).点P是y轴右侧抛物线上一动点(不与点A重合),过点P作直线PC⊥x轴于点C,PD⊥y轴与点D,设矩形PCOD的周长为l,点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图上1厘米代表实际距离100千米 | B. | $\frac{1}{50000}$ | ||
| C. | 五十万分之一 | D. | 1:1000000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
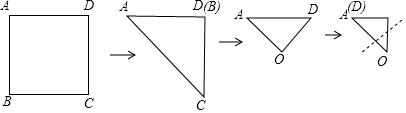
| A. | 等腰直角三角形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20元 | B. | 24元 | C. | 30元 | D. | 36元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com