
【题目】类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.

【答案】(1)130°,80°;(2)①证明见解析;②不正确,反例见解析;(3)![]() 或
或![]() .
.
【解析】
试题(1)根据定义和四边形内角和定理求解即可.
(2)①连接BD,根据定义以及等腰三角形的判定和性质求证即可.
②当相等角的两边相等时,结论不正确.
(3)分∠ADC=∠ABC=90°和∠BCD=∠DAB=60°两种情况讨论即可.
试题解析:(1)∵等对角四边形ABCD中,∠A≠∠C,∠B=80°,∴∠D=∠B=80°.
∵∠A=70°,∴![]() .
.
(2)①如图,连接BD,
∵AB=AD,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴CB=CD.

②不正确,反例如图,∠A=∠C=90°,AB=AD,但CB≠CD.

(3)①如图,当∠ADC=∠ABC=90°时,延长AD,BC交于点F,
∵∠ABC=90°,∠DAB=60°,AB=5,∴AE=10.
∴![]() .
.
∵∠EDC=90°,∠E=30°,∴![]() .
.
∴![]() .
.

②如图,当∠BCD=∠DAB=60°时,过D点作DE⊥AB于点E,DF⊥BC于点F,
∵DE⊥AB,∠DAB=60°,AD=4,∴![]() .
.
∴![]() .
.
∵四边形BFDE是矩形,∵![]() .
.
∵∠BCD=60°,∴![]() .∴
.∴![]() .
.
∴![]()



科目:初中数学 来源: 题型:
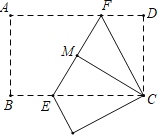
【题目】如图,把一张矩形纸片折叠,点A与点C重合,折痕为EF,再将△CDF沿CF折叠,点D恰好落在EF上的点M处,若BC=6厘米,则EF的长为_____厘米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生会要举办一个校园书画艺术展览会,为国庆献礼,小华和小刚准备将长AD为400cm,宽AB为130cm的矩形作品四周镶上彩色纸边装饰,如图所示,两人在设计时要求内外两个矩形相似,矩形作品面积是总面积的![]() ,他们一致认为上下彩色纸边要等宽,左右彩色纸边要等宽,这样效果最好,请你帮助他们设计彩色纸边宽度.
,他们一致认为上下彩色纸边要等宽,左右彩色纸边要等宽,这样效果最好,请你帮助他们设计彩色纸边宽度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:
销售单价(元) | 40+x |
销售量y(件) |
|
销售玩具获得利润W(元) |
|
(2)在(1)问条件下,若商场获得10000元销售利润,则该玩具销售单价应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )

A. DE=EB B. ![]() DE=EB C.
DE=EB C. ![]() DE=DO D. DE=OB
DE=DO D. DE=OB
查看答案和解析>>
科目:初中数学 来源: 题型:
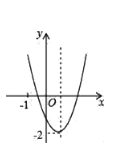
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
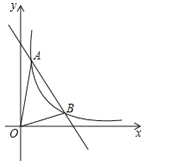
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为⊙
为⊙![]() 上一点,
上一点,![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.
(1)试判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若⊙![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
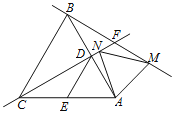
【题目】如图,等边△ABC中,边长为6,D、E分别是AB、AC的中点,连接DE,将△ADE绕点A顺时针旋转得到△AMN,其中D、E的对应点分别是M、N,直线BM与直线CN交于点F,若旋转360°,则点F经过的路径长是( )
A.![]() B.8
B.8![]() C.
C.![]() D.4
D.4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com