
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,AD边上,若AM:MB=AN:ND=1:2,则sin∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
【答案】B
【解析】解:∵AB=AD=6,AM:MB=AN:ND=1:2, ∴AM=AN=2,BM=DN=4,
连接MN,连接AC,
∵AB⊥BC,AD⊥CD,∠BAD=60°
在Rt△ABC与Rt△ADC中,![]() ,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAC=∠DAC= ![]() ∠BAD=30°,MC=NC,
∠BAD=30°,MC=NC,
∴BC= ![]() AC,
AC,
∴AC2=BC2+AB2 , 即(2BC)2=BC2+AB2 ,
3BC2=AB2 ,
∴BC=2 ![]() ,
,
在Rt△BMC中,CM= ![]() =2
=2 ![]() ,
,
∵AN=AM,∠MAN=60°,
∴△MAN是等边三角形,
∴MN=AM=AN=2,
过M点作ME⊥CN于E,设NE=x,则CE=2 ![]() ﹣x,
﹣x,
∴MN2﹣NE2=MC2﹣EC2 , 即4﹣x2=(2 ![]() )2﹣(2
)2﹣(2 ![]() ﹣x)2 ,
﹣x)2 ,
解得:x= ![]() ,
,
∴EC=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
由勾股定理得:ME= ![]() =
= ![]() =
= ![]() ,
,
∴sin∠MCN= ![]() =
= ![]() =
= ![]() ,
,
故选B.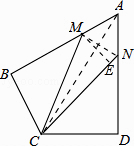
【考点精析】掌握相似三角形的判定与性质和解直角三角形是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是 , cosA的值是 . (结果保留根号) 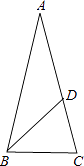
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城市群的建设与发展,在A,B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的120km缩短至114km,城际铁路的设计平均时速要比现行的平均时速快110km,运行时间仅是现行时间的![]() ,求建成后的城际铁路在A,B两地的运行时间.
,求建成后的城际铁路在A,B两地的运行时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A=![]() .
.
(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4)……解关于x的不等式:![]() -
-![]() ≤f(3)+f(4)+…+f(11),并将它的解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将它的解集在数轴上表示出来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1 , a2 , …,a2017是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2017=84,(a1+1)2+(a2+1)2+…+(a2017+1)2=4001,则a1 , a2 , …,a2017中为0的个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶油的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com