
 四边形ABCD中,AB=BC,BC∥AD,∠ABC=90°,点E为DC上一点,且AE=AB,AM平分∠DAE交BE的延长线于M,连接CM.
四边形ABCD中,AB=BC,BC∥AD,∠ABC=90°,点E为DC上一点,且AE=AB,AM平分∠DAE交BE的延长线于M,连接CM.分析 (1)过点A作AF⊥MB于点F,交BC于点G,因为∠ABC=90°,根据同角的余角相等及等腰三角形“三线合一”的性质不难得到∠BAE=2∠MBC,
(2)由AM平分∠DAF及AF平分∠EAB及∠DAB=90°,得∠MAF=45°,从而得到∠AMF=45°,进一步证得△AFM为等腰三角形,延长AG到H,使AH=MB,通过证△ABH≌△BCM,所以FB=FH,∠FHB=∠FBH=45°,因此∠CMB=∠AMB=45°,结论得证,
(3)若∠MBC=30°,则∠BAF=30°,在Rt△BFA中,30°角所对的直角边等于斜边的一半,种用勾股定理求出AF的长及MF的长,所以ME=MF-EF可求解.
解答 (1)证明: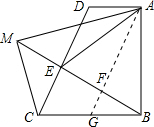 过点A作AF⊥MB于点F,交BC于点G,
过点A作AF⊥MB于点F,交BC于点G,
∵AE=AB,
∴∠EAG=∠BAG=$\frac{1}{2}$∠BAE,
∵∠ABC=90°,∠ABF+∠GFB=90°,
又∠FAB+∠ABF=90°,
∴∠FBG=∠FAB即:∠MBC=∠GAB=$\frac{1}{2}$∠BAE,
∴∠BAE=2∠MBC.
(2延长AG到H使AH=MB,连结BH,
∵BC=AB,∠CBM=∠HAB,
∴△MCB≌△HBA
∴∠BMC=∠AHB
∵AD平分∠DAE,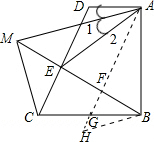 ∴∠1=$\frac{1}{2}$∠DAE,
∴∠1=$\frac{1}{2}$∠DAE,
又∠2=$\frac{1}{2}$∠EAB,
∴∠MAF=∠1+∠2=$\frac{1}{2}$(∠DAE+∠EAB)=$\frac{1}{2}$∠DAB$\frac{1}{2}$×90°=45°,
∵∠AFE=90°,
∴∠AMB=90°-∠MAF=90°-45°=45°,
∴∠AMB=∠MAB,
∴FM=FA,
∴MB-FM=AH-AF,即:FB=FH,
∴∠FHB=∠FBH=45°,
∴∠AMB=∠FBH
∴∠CMB=∠AMB
∴MB平分∠AMC,
(3)如右上题图,若∠MBC=30°,则∠FAB=30°,
在Rt△ABF中,EF=FB=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2
∴AF=$\sqrt{A{B}^{2}-F{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵MF=AF=2$\sqrt{3}$,
∴ME=MF-EF=2$\sqrt{3}$-2.
点评 本题主要考查直角三角形的性质及全等三角形的判定及性质,等腰三角形的性质及辅助线的正确运用是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:选择题
 如图,⊙O的直径AB=12,弦CD⊥AB,∠C=30°,则S阴影等于( )
如图,⊙O的直径AB=12,弦CD⊥AB,∠C=30°,则S阴影等于( )| A. | 6π | B. | 2π | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,反比例函数y=$\frac{9}{x}$的图象过边长是a(图中最小正方形边长为a且为整数)的正方形网格上的A、B两点,则a的值是( )
如图,反比例函数y=$\frac{9}{x}$的图象过边长是a(图中最小正方形边长为a且为整数)的正方形网格上的A、B两点,则a的值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,∠C=120°,CD=4,按以下步骤作图:
如图,在?ABCD中,∠C=120°,CD=4,按以下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 83 | 80 | 83 | 75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com