
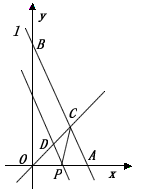
| 解:(1)设直线l解析式为y=kx+b, 将A(6,0)和B(0,12)代入, 得:  , ,解得:  , , ∴直线l解析式为y=-2x+12; |
|
(2)解方程组: , ,得: 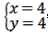 , , ∴点C的坐标为(4,4), ∴S△COP=  x×4=2x; x×4=2x; ∵PD∥l, ∴△OPD∽△OAC, ∴ 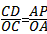 , ,而 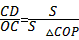 , ,∴  , ,即 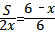 , ,∴△PCD的面积S与x的函数关系式为: S=-  x2+2x, x2+2x, ∵S=- 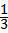 (x-3)2+3, (x-3)2+3, ∴当x=3时,S有最大值,最大值是3; |
 |
| (3)存在点P,使得△PCA成为等腰三角形, ∵点C的坐标为(4,4),A(6,0), 根据P1C=CA,P3A=AC,P2A=AC,P4C=P4A时分别求出即可, 当P1C=CA时,P1(2,0), 当P2A=AC时,P2(6-2 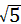 ,0), ,0),当P3A=AC时,P3(6+2 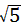 ,0), ,0),当P4C=P4A时,P4(1,0), ∴点P的坐标分别为: P1(2,0),P2(6-2,0),P3(6+2 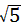 ,0),P4(1,0)。 ,0),P4(1,0)。 |


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com