练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
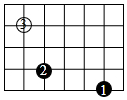
    17．如图，在围棋盘上有三枚棋子，如果黑棋①的位置用有序数对（0，-1）表示，黑棋②的位置用有序数对（-3，0）表示，则白棋③的位置可用有序数对（　　）表示．
    A．（-2，4）B．（2，-4）C．（4，-2）D．（-4，2）

    分析 根据黑棋①的坐标向上1个单位确定出坐标原点，然后建立平面直角坐标系，再写出白棋③的坐标即可．

    解答 解：建立平面直角坐标系如图，
    白棋③的坐标为（-4，2）．
    故选D．

    点评 本题考查了坐标确定位置，根据已知点的坐标确定出坐标原点的位置是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．一组数据：1，4，x，3 的平均数是3，则这组数据的中位数是（　　）
    A．3B．3.5C．4D．4.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图所示的几何体是由6个完全相同的小正方体组成的，则下面四个平面图形中不是这个几何体的三视图的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．目前，谷歌人工智能AlphaGo机器人引起了人们的广泛关注，某教学网站开设了有关人工智能的课程并策划了A，B两种网上学习的月收费方式：
    收费方式月使用费（元）包月上网时间（h）超时费（元/h）
    A7253.6
    B10504.8
    设小明每月上网学习人工智能课程的时间为x小时，方案A，B的收费金额分别为yA元，yB元．
    （1）当x≥50时，分别求出yA，yB与x之间的函数关系式；
    （2）若小明3月份上该网站学习的时间为60小时，则他选择哪种方式上网学习更合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

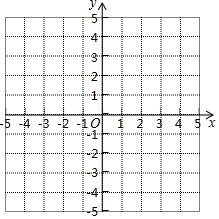    12．一般地，二元一次方程的解可以转化为点的坐标，其中x的值对应为点的横坐标，y的值对应为点的纵坐标，如二元一次方程x-2y=0的解$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$和$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$可以转化为点的坐标A（0，0）和B（2，1）．以方程x-2y=0的解为坐标的点的全体叫做方程x-2y=0的图象．
    （1）写出二元一次方程x-2y=0的任意一组解$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$，并把它转化为点C的坐标（-2，-1）；
    （2）在平面直角坐标系中，任何一个二元一次方程的图象都是一条直线，如方程x-2y=0的图象是由该方程所有的解转化成的点组成，在图中描出点A、点B和点C，观察它们是否在同一直线上；
    （3）取满足二元一次方程x+y=3的两个解，并把它们转化成点的坐标，画出二元一次方程x+y=3的图象；
    （4）根据图象，写出二元一次方程x-2y=0的图象和二元一次方程x+y=3的图象的交点坐标（2，1），由此可得二元一次方程组$\left\{\begin{array}{l}{x-2y=0}\\{x+y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图①，在四边形ABCD中，AD∥BC，AB=8cm，AD=16cm，BC=22cm，∠ABC=90°，点P从点A出发，以1cm/s的速度向点D运动，点Q从点C同时出发，以3cm/s的速度向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t秒．
    （1）当t为何值时，四边形ABQP成为矩形？
    （2）当为何值时，以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形？
    （3）四边形PBQD是否能成为菱形？若能，求出t的值；若不能，请说明理由，并探究如何改变Q点的速度（匀速运动），使四边形PBQD在某一时刻为菱形，求点Q的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）阅读下列内容并回答问题：
    问题：在平面直角坐标系xOy中，将直线y=-2x向上平移3个单位，求平移后直线的解析式．
    小雯同学在做这类问题时经常困惑和纠结，她做此题的简要过程和反思如下．

    在课堂交流中，小谢同学听了她的困惑后，给她提出了下面的建议：“你可以找直线上的关键点，比如点A（1，-2），先把它按要求平移到相应的对应点A′，再用老师教过的待定系数法求过点A′的新直线的解析式，这样就不用纠结了．”
    小雯用这个方法进行了尝试，点A（1，-2）向上平移3个单位后的对应点A′的坐标为（1，1），过点A′的直线的解析式为y=-2x+3．
    （2）小雯又提出了一个新问题请全班同学一起解答和检验此方法，请你也试试看：
    将直线y=-2x向右平移1个单位，平移后直线的解析式为y=-2x+1，另外直接将直线y=-2x向上（填“上”或“下”）平移1个单位也能得到这条直线．
    （3）请你继续利用这个方法解决问题：
    对于平面直角坐标系xOy内的图形M，将图形M上所有点都向上平移3个单位，再向右平移1个单位，我们把这个过程称为图形M的一次“斜平移”，求将直线y=-2x进行两次“斜平移”后得到的直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

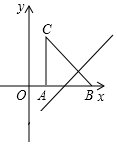    6．如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0）．
    （1）点C的坐标是（1，4）；
    （2）将△ABC沿x轴向右平移，当点C落在直线y=2x-6上时，线段AC扫过的面积为16．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

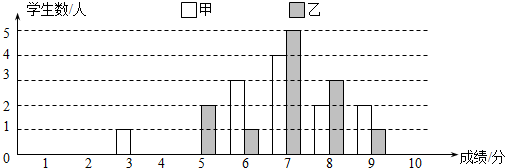
    7．我校九年级理化实验的一次测验，学生得分均为整数，满分为10法，成绩达到6分以上（包括6分）为合格，成绩达到9分为优秀，这次测验甲、乙两组学生成绩分布的条形统计图如下：

    （1）请补充完整下面的成绩统计分析表：
    平均分方差中位数合格率优秀率
    甲组6.92.4791.7%16.7%
    乙组71.3783.3%8.3%
    （2）你认为那一组同学的成绩较好，至少说出两条选择的理由．

    查看答案和解析>>

    同步练习册答案