
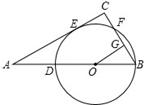
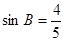 ,求线段AD的长.
,求线段AD的长.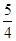
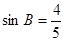 ,可求得AB的长,易证得△AEO∽△ACB,然后根据相似三角形的对应边成比例,可求得OB的长,继而求得AD的长.
,可求得AB的长,易证得△AEO∽△ACB,然后根据相似三角形的对应边成比例,可求得OB的长,继而求得AD的长.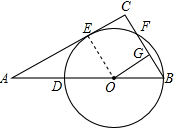
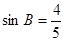
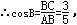
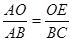 ,即
,即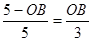 ,解得
,解得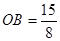
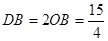
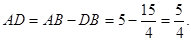


科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
 时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留
时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留 );
);查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com