练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知：∠MON=132°，射线OC是∠MON内一条射线，且
    1
    3
    ∠CON+
    1
    2
    ∠MOC=59度．问OM与OC是否垂直，并说明理由．
    分析：由已知可得∠CON+∠MOC=132°，再根据
    1
    3
    ∠CON+
    1
    2
    ∠MOC=59°，就可以得到一个关于∠CON与∠MOC的方程组，解出∠MOC的值，就可以判断OM与OC的位置关系．
    解答：解：OM⊥OC．
    理由如下：
    设∠CON为x°，则∠MOC为（132-x）°，
    依题意，得
    1
    3
    x+
    1
    2
    (132-x)=59    ，
    解得x=42．
    ∴∠MOC=∠MON-∠CON=132°-x=132°-42°=90°，
    即OM⊥OC．
    点评：把角的关系转化为方程来解，是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

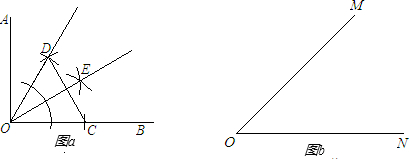
    （1）“三等分角”是数学史上一个著名问题，但数学家已经证明，仅用尺规不可能“三等分任意角”．但对于特定度数的已知角，如90°角、45°角等，是可以用尺规进行三等分的．如图a，∠AOB=90°，我们在边OB上取一点C，用尺规以OC为一边向∠AOB内部作等边△OCD，作射线OD，再用尺规作出∠DOB的角平分线OE，则射线OD、OE将∠AOB三等分．仔细体会一下其中的道理，然后用尺规把图b中的∠MON三等分（已知∠MON=45°）．（不需写作法，但需保留作图痕迹，允许适当添加文字的说明）
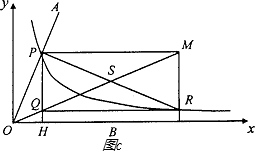
    精英家教网
    （2）数学家帕普斯借助函数给出了一种“三等分锐角”的方法（如图c）：将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上、边OA与函数y=
    1
    x
    的图象交于点P，以P为圆心、2OP长为半径作弧交图象于点R．分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=
    1
    3
    ∠AOB．要明白帕普斯的方法，请研究以下问题：
    ①设P（a，
    1
    a
    ）、R（b，
    1
    b
    ），求直线OM对应的函数关系式（用含a、b的代数式表示）．
    ②分别过点P和R作y轴和x轴的平行线，两直线相交于点Q．请说明Q点在直线OM上，并据此证明∠MOB=
    1
    3
    ∠AOB．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：同步训练与评价·数学·七年级·上 题型：044

    下图为2003年某月的日历：

    Sun

    Mon

    Tue

    Wed

    Thu

    Fri

    Sat
    　 　 　

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    31

    		 　

    (1)在日历上，任意圈出一个竖列上相邻的3个数；

    ①设中间的一个数为a，则另外的两个数为________，________

    ②若已知这三个数的和为45，则这三天分别是________，________，________号，它们都在星期________

    (2)在日历上，任意圈出一个竖列上相邻的4个数；

    ①设最大一个数为b，则另外三个数为________、________、________

    ②若已知这4个数的和为66，则这四天分别是________，________，________，________号，它们都在星期________

    查看答案和解析>>

    同步练习册答案