
分析 分类讨论:当点E在AD上,如图1,连结BD交AC于O点,根据菱形的性质得∴AB=BC=AD=6,BC∥AD,AB∥CD,AC⊥BD,OA=OC,易得△ABD为等边三角形,则AO=$\frac{\sqrt{3}}{2}$AB=3$\sqrt{3}$,所以AC=2AO=6$\sqrt{3}$,再利用BC∥AE得到△BCM∽△EAM,利用相似比可得$\frac{MC}{AM}$=$\frac{BC}{AE}$=2,然后根据比例得性质可计算出MC的长;当E点在AD的延长线上时,如图2,则AE=AD+DE=9,同理可得△BCM∽△EAM,利用相似比得$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{2}{3}$,然后根据比例性质计算MC的长.
解答 解:当点E在AD上,如图1,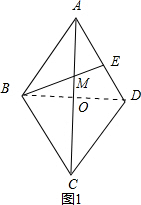

连结BD交AC于O点,
∵四边形ABCD为菱形,
∴AB=BC=AD=6,BC∥AD,AB∥CD,AC⊥BD,OA=OC,
∵∠ADC=120°,
∴∠BAD=60°,
∴△ABD为等边三角形,
∴AO=$\frac{\sqrt{3}}{2}$AB=3$\sqrt{3}$,
∴AC=2AO=6$\sqrt{3}$,
而DE=3,
∴AE=3,
∵BC∥AE,
∴△BCM∽△EAM,
∴$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{6}{3}$=2,
∴$\frac{MC}{AC}$=$\frac{2}{3}$,
∴MC=$\frac{2}{3}$×6$\sqrt{3}$=4$\sqrt{3}$;
当E点在AD的延长线上时,如图2,则AE=AD+DE=9,
∵BC∥AE,
∴△BCM∽△EAM,
∴$\frac{MC}{AM}$=$\frac{BC}{AE}$=$\frac{6}{9}$=$\frac{2}{3}$,
∴$\frac{MC}{AC}$=$\frac{2}{5}$,
∴MC=$\frac{2}{5}$×6$\sqrt{3}$=$\frac{12\sqrt{3}}{5}$,
综上所述,CM的长为4$\sqrt{3}$或$\frac{12\sqrt{3}}{5}$.
故答案为4$\sqrt{3}$或$\frac{12\sqrt{3}}{5}$.
点评 本题考查了菱形性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了相似三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
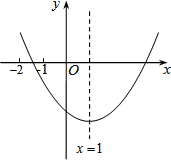 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆的切线必垂直于半径 | B. | 垂直于切线的直线必经过圆心 | ||
| C. | 垂直于切线的直线必经过切点 | D. | 圆的切线垂直于经过切点的半径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
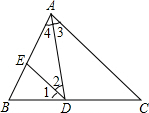 请在括号里填上推理的根据
请在括号里填上推理的根据查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛一枚硬币,正面朝上 | |
| B. | 抛一颗骰子,点数不大于6 | |
| C. | 到电影院任意买一张电影票,座位号是奇数 | |
| D. | 打开电视机,任选一个频道,屏幕上正在播放天气预报 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com